Photometry Method

 

The photometric procedure I use in my studies is divided between these sections:

Observations

Reduction

Measurements

Calibration

Analysis

 

 

Observations

            When choosing the targets, some observational limitations were considered due to specific physical restrictions and magnitude limitations:

  1. Declination: The C18 cannot observe more south than δ=-34o due to the structure of its fork mount. The 1-m telescope can reach as far south as declination -40o.
  2. Hour angle: To avoid complex calibration processes due to atmospheric light extinction, the observations were strict to an air mass of 2.5 and below.
  3. Angular velocity limitation on field of view: when NEAs with fast angular velocities were observed, the field of view of the CCD was taken under consideration, so the asteroid would cross the field without requiring the changing of the telescope pointing during the night. In some cases, only the C18 CCDs with a large field of view were used.
  4. Angular velocity limitation on exposure time: to produce an approximately circular shape for the observed asteroids' PSF and to avoid the smearing of the light, time exposures (tmax) were limited by the angular velocity (v) of the asteroid by:

tmax = FWHM / v                                                                                 (1)
when FWHM is the Full Width Half Maximum of the target, which is usually determine by the seeing condition at the observatory, and ranges between 2.5 to 3 arcsec. Thus, an average MBA with a typical angular velocity smaller than 0.01 ''/sec could be easily observed for 3 to 4 minutes without smearing, while an NEA with a much faster angular velocity, 0.01 ''/sec to 0.05 ''/sec, could only be observed for  60 to 90 seconds.

  1. Magnitude limitation: the observed brightness of asteroids varies as their non-spherical shape rotates, when a colored spot on their surface with different albedo enters the line of sight, or when a satellite obscures part of its reflected light. Usually, such variations are in the order of a few tenths of a magnitude, with some exceptions toward a hundredth of a magnitude at the faint end, and a full magnitude at the bright end. Therefore, when choosing an exposure time, one should bear in mind that sufficient photons should be collected so that the measurement errors will not exceed a few hundredths of a magnitude. One solution is too increase the exposure time for asteroids with a fainter signal, although this is limited by the angular velocity of the asteroid (see the section above), by the increasing number of cosmic rays collected by the CCD, by the dark current of the CCD that add noise, and by the number of tracking and guiding problems that increase with exposure time. After extensive use of the Wise Observatory equipment, we found that when using exposure times of 180 seconds, asteroids with a V magnitude brighter than 17 have photometric errors of order of 0.01 to 0.05 mag., while asteroids with 17 < m < 18 mag. have photometric errors of 0.05 - 0.1 magnitude. Between 18 to 19 magnitudes the photometric quality deteriorates rapidly, while at 19 mag. the asteroids can barely be seen.
  2. Bright nights, with a Moon 70% full and larger, were avoided. In addition, only asteroids that were sufficiently distant from the Moon (as a function of the Moon phase) were observed.
  3. Asteroids that crossed the galactic plane (at ±15o) were also avoided. Such objects are very hard to measure because the light from the crowded background cannot be easily calibrated.
  4. No observations were performed on nights with high humidity, heavy clouds or strong wind.

 

 

Reduction

            The images were reduced in a standard manner using the Image Reduction and Analysis Facility (IRAF) and the SAOImage DS9 viewer program. The reduction included the following procedures.

 

Bias subtraction

Between 5 to 10 bias images with zero exposure time were obtained during each night. An averaged bias image was created by the nightly bias images using a median procedure, followed by its subtraction from all the images taken during the same night. The different bias values for each CCD are summarized in the next Table.

 

Bias values for each CCD

CCD

Tek

SITe

PI

SBIG ST-10XME

SBIG STL-6303E

Average count

485

240

115

105

900

Std.Dev.

6.5

12

2.87

10

15

 

Dark subtraction

Since the C18 telescope is not equipped with cryogenically-cooled CCD, but with only thermoelectrically-cooled ones, removing the dark current was essential. Four or five dark images with closed shutter were obtained in each night with exposure times equal  to those of the nightly observations. Averaged dark images, one for each exposure time, were created by the nightly dark images using a median procedure, followed by their subtraction from all the images obtained during the same night.

 

Flat Field correction

During the evening and/or morning twilight of each night 4 to 7 flat field sky images were observed using exposure times of 3 to 60 seconds. These allowed the derivation of flat-field (FF) images with 20,000 to 40,000 counts per pixel. The FF images were bias and dark subtracted and were combined by a median average, followed by its normalization by the average count of the combined flat field image to yield an image with values near unity. This procedure was performed separately for FF images taken with different filters. All of the images of the night, after being bias and dark subtracted, were divided by the normalized FFs. If FF images were not taken during twilight of the specific night (usually due to bad weather) the FF images of the previous or following night were used.

            Some observations in 2005-2006, performed with the 1-m telescope, were reduced using dome flats. These were obtained by observing a uniformly illuminated white surface inside the dome instead of observing the twilight sky. Since the illumination was not uniform, these FF images contained too much noise, therefore this procedure was discarded.

 

Time correction

Observing times were corrected from the recorded time of beginning to the mid-exposure to reflect the real time of the image.

 

Finding stars and alignment

The IRAF daofind function was used to find the X,Y coordinates of the stars in each image. The list of stars and their coordinates were later used to align all the images of the same field in order that the photometry of the reference stars could be done automatically, and for easy recognition of the moving asteroids. The alignment procedure used the IRAF functions of xyxymatch, geomap and geotran. The transformation of the images was done only in the X, Y directions because rotational alignment was found not to be necessary.

 

Astrometry and asteroids Identification

The large field of view of the C18's CCDs allows many asteroids to be caught in the frame while observing a specific asteroid, especially if it orbits the Sun in the main belt of asteroids. In some cases, up to 15 asteroids were observed in the same field of view. Therefore, observations with the C18 are usually followed by an astrometric solution of the plate by the PinPoint Engine software (www.dc3.com) obtained by comparing the image to an USNO.A2 catalogue immediately following the reading out of the chip. At the reduction phase, the astrometric solutions were read for any moving object in the plate and were compared to the Minor Planet Center (MPC) web database for identification.

 

 

Measurements

The phot function of IRAF was used for the photometric measurements. The asteroids were manually and interactively recognized and measured by the user at each image while the reference stars were automatically measured using their locations on the plate as been found by the daofind function. The centeroid algorithm was used to better determine the centers of the asteroid and reference stars’ images. Apertures with a radius of four pixels were chosen, to minimize photometric errors. The mean sky value was measured using an annulus of 10 pixels width and inner radius 10 pixels wide centered on the asteroid. The flux and magnitudes of the measured objects were calculated in a standard way by the IRAF phot function using:

Flux = (Counts – area · mean sky) / exposure time                                            (2)

Magnitude = – 2.5·log(Flux) + Zero Point                                                         (3)

The magnitude error (ΔM) is a function of the measured counts, the area of the aperture, the number of sky pixels (nSky), the std.dev of the sky and the gain value (electrons per adu):

ΔM = 1.0857 ·  / Counts     (4)

 

 

Calibration

Relative calibration

After measuring, the photometric values were calibrated to a differential magnitude level using up to a thousand local comparison stars measured automatically on every image by the same method as the asteroid. A photometric shift was calculated for each image compared to a good reference image, using the local comparison stars. Stars that appeared variable were removed at a second calibration stage leaving on average a few hundred local comparison stars per image observed by the C18. The 1-m CCDs have a much smaller field of view, thus only some tens of objects were used as good local comparison stars. The brightness of these stars remained constant to ±0.02 mag.

 

Absolute calibration

In some cases, where possible and required for further studies, the instrumental photometric values were calibrated to standard magnitudes using measurements of Landolt equatorial standards (Landolt 1992). These were observed at air masses between 1.1 to 2.5 while switching between the asteroid fields that included local comparison stars used for the relative calibration. Landolt standards were observed only on specific nights and only under photometric conditions. The extinction coefficients for the photometric nights, including the zero point, were obtained using the Landolt standards after measuring them in a ten-pixel radius aperture. From these, standard magnitudes of the local comparison stars in each field were derived, followed by calculating the magnitude shift between the daily weighted-mean magnitude and the catalog magnitude of the comparison stars. This magnitude shift was added to the data of the relevant field and asteroids, and introduced an additional error of ~0.02-0.03 mag due to the observational systematic errors of the standards and the comparison stars, and due to uncertainties in matching the photometric coefficients. For the C18 images, that were obtained in white light, we used the Cousins R magnitudes of the Landolt standards for the calibration since the "Clear" filter is similar to a very wide R band. We note that the accepted range of asteroidal colors was included in the wide color range of the observed standards (-0.03 ≤ B-V ≤ 1.1) removing possible color biases, and the color term of our transformation from instrumental to Cousins R was smaller than 0.01 mag.

 

Time and distance calibration

To be able to work on data from different nights the asteroid magnitudes were corrected for light travel time using:

JDastj = JDobsj – Δ j/c                                                                                     (5)

when Δj is the Earth-asteroid distance for image j, JDobsj is the Julian date of the observed image, JDastj is the corrected Julian date for the asteroid and c is the speed of light.

The magnitudes were reduced to a 1 AU distance from the Sun and the Earth to allow the data to be folded by the rotational period of the asteroid. This yields the reduced magnitude values (Bowell et al. 1989):

V(1,α) = M – 5·log(rj·Δj)                                                                                  (6)

when M is the calibrated magnitude of the asteroid in image j, rj and Δj are the heliocentric and geocentric distances of the asteroid, respectively, at the time image j was obtained and V(1,α) is the reduced magnitude of the asteroid at 1 AU at a α phase angle.

 

 

Analysis

            An asteroid lightcurve (LC) can provide valuable insights about the asteroid properties: brightness is a function of the asteroid size; LC periodicity coincides with spin; shape can be determined by examining the lightcurve amplitude; axis orientation is derived by studying changes in the height and shape of the LC at different viewing geometries; colors of asteroids provide indication of their spectral type and composition; special features in the LCs, such as eclipses and occultations, may imply binarity and shed light on internal structure and density. For this study we used different analyses to derive different properties of the observed asteroids, as described below.

 

Finding the asteroid periodicity

The asteroid rotation is usually detected as periodic changes in brightness; these are produced by the asteroid presenting areas of different sizes of its “ellipsoidal” shape to the observer thus changing the flux of reflected sunlight. Colored spots, or unique surface structures, can also become noticeable in the photometric lightcurve, exhibiting the rotation frequency of the asteroid. The period can be derived using a Fourier series expansion of the brightness modulation (Harris and Lupishko 1989):

V(α,t) = H(α) + {Bn·sin[ (2πn/P)·(t-t0) ]+ Cn·cos[ (2πn/P)·(t-t0) ]}   (7)

when V(α,t) is the reduced magnitude of the asteroid at 1 AU distance from the Sun and the Earth at time t and phase angle α, H(α) is the mean reduced magnitude at one period, Bn and Cn are Fourier coefficients of order n, P is the rotation period and t0 is the epoch. A best match of the observations to Eq. 7 is found by least squares:

                                                                                                (8)

In cases where the magnitudes were not calibrated to a standard level, data from different nights were shifted to derive a good-matching periodicity model. This procedure worked out well for objects whose measurements fully covered the frequency of the lightcurve for at least one night. When the rotation period of the asteroid was longer than the nightly observing time and parts of the lightcurve were never observed in the same night, i.e. they were not calibrated between themselves, deriving the magnitude shift between different nights was not trivial. Here, different possibilities for magnitude shift were checked and the best option was found by least squares.

Most asteroids were analyzed using only two harmonics to fit the data to a simple model. In these cases the model may not fit second-order features of the LC. In some cases, where many measurements with small errors were available, we fitted the data using a model with more harmonics ranging from 3 to 10. The error of the derived period was determined to be 1-σ of the best-fitted frequency.

 

Constraining the asteroid shape

Constraints on asteroid shapes were derived from the amplitude of the folded lightcurve, assuming a triaxial body with physical axes of a ≥ b ≥ c as the object rotation is about the c axis (Harris and Lupishko 1989). At the first step, the amplitude A(α) was calibrated to zero phase angle A(00) using the method of Zappala et al. (1990):

A(00) = A(α) / (1 + m∙α)                                                                                   (9)

where α is the phase angle and m is the slope that correlates the amplitude with the phase angle. We used the average value of m=0.023 deg-1 found by Zappala et al. (1990) from 27 different measurements. Using the calibrated amplitude A(00), we calculated a minimum value for the axial ratio a/b using:

A(00) = 2.5·log                                                                                     (10).

 

Deriving the phase angle coefficients

            The phase angle is defined as the Earth-Asteroid-Sun angle. While at zero phase angle the asteroid phase is “full” and the body is at its brightest, as the phase angle increases the brightness of the asteroid decreases following a slope which is a function of the illumination properties of the asteroid's surface (such as albedo, composition and more). The brightest magnitude of the asteroid (averaged over its rotation period) is defined as the absolute magnitude H, while the slope is determine by a mathematical constant called the “phase slope” and marked by the letter G. The decreasing mean magnitude of an asteroid (for one rotation period) as a function of its phase angle is described by (Bowell et al. 1989):

H(α) = H – 2.5·log[(1-G)·Φ1(α) + G·Φ2(α)]                                                      (11)

when H(α) is the mean reduced magnitude during one rotational period at phase angle α and Φ1 and Φ2 are two functions that describe the light scattering from a single particle (Φ1) and from many particles (Φ2) using:

A1 = 3.332                   A2 = 1.862                                                                   (12)

B1 = 0.631                   B2 = 1.218

C1 = 0.986                   C2 = 0.238

W = exp(-90.56·[tan2(0.5·α)])                          i = 1,2

φ iL = exp(-Ai·[tanBi(0.5·α)])

φ iS = 1 -

Φ i = W·φiS + (1 - W)·φiL

 

            The absolute magnitudes were derived for cases were the data was calibrated to a standard level. The G slope was fitted to the data if a reasonably wide range (>10o) of phase angles was observed. To better constrain our results the H-G systems were fitted to the data together with the periodicity search using the sum of equations (3.7 and 3.11):

V(α,t) + 2.5·log[(1-G)·Φ1(α)+G·Φ2(α)] = H + {Bn·sin[()·(t-t0)]+Cn·cos[()·(t-t0)]}      (13)

A chi-square surface plotted against f = 2nπ/P and G provides the best f and G and allows the determination of the error as one standard deviation from the minimum. An example is shown in Fig. 3.3, followed by the fit of the spin model to the observations (Fig. 3.4). Since most asteroids described here were not observed over a wide phase angle range, we used a default value of G=0.15±0.12. The error of the G slope in this general case is the standard deviation of many G values found in the study of Lagerkvist and Magnusson (1990; see their Table II, third column). For asteroids observed at small phase angles, this G slope error introduces an error of about 0.08 magnitudes to the absolute magnitude H.

 

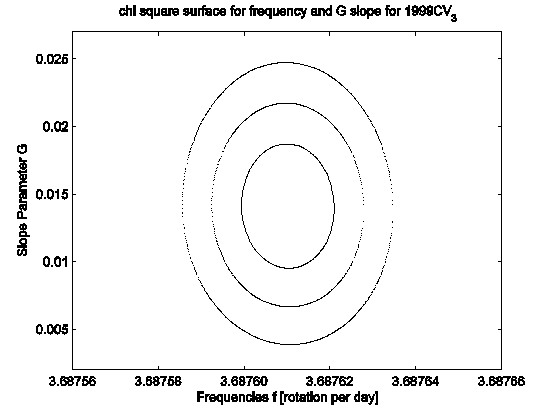
A chi-square surface for different f and G values for the case of (11405) 1999 CV3. The contours stand for one sigma (68% confidence level, inner full curve), two sigma (95%, dashed curve) and three sigma (99.7%, dots).

 

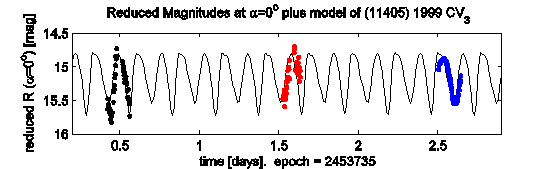
Lightcurve model fit to the observed data for December 30, 2005 to January 1, 2006 of (11405) 1999 CV3.

 

Estimating the size of the asteroid

            Given the absolute magnitude H of the asteroid (defined at 1 AU from the Sun and the Earth), one can estimate the effective radius R of the asteroid, which is the radius for a hypothetical spherical object, using:

                                                                                             (14)

While Eq. 14 is used for magnitudes in the V band, most of the observations reported here were taken with no filter. This, as mentioned above and as detailed in Brosch et al. (2008), corresponds to a wide-R band. Therefore, unless a direct measurement of the asteroid colors was available, a color of V-R = 0.45 mag was assumed to translate the measured HR to HV magnitudes (HV = H), in a consistent way with the method of Pravec et al. (1998). Since a color variation of ±0.1 mag may change the diameter estimate by less than five percent, the observed asteroids would still be in the size range reported here and such color variations can be neglected.

Albedo values run from ~0.05 for dark carbonaceous asteroids up to ~0.5 for the shiniest "metal" surfaces of the E-type asteroids. To obtain an exact albedo value astronomers use far-infrared (FIR) measurements and check the ratio between the FIR emitted flux to measurements taken in visible light. However, this method is beyond the scope of this study. To use a reliable albedo value, the dark C-type asteroids were assumed to be more common in the outer regions of the MB than S-types. Although recent studies differ about the heliocentric distance where the transition takes place (Bus and Binzel 2002, Mothé-Diniz et al. 2003), we followed the estimate that S-type asteroids are the majority at the inner main belt (Gradie and Tedesco 1982). For simplicity, we chose an albedo of 0.2 for asteroids from the inner main belt, 0.10 for asteroids from the central main belt and 0.058 for asteroids from the outer main belt. For consistency, we followed the Harris and Warner region definition as appears in their lightcurve database. Asteroids from a distinct family or group (like the Flora group) received the average albedo of the group.

We did not use a higher albedo for the inner MBAs in order to retain a conservative, not-too-small, estimate for the diameters of these asteroids. One should, therefore, keep in mind that these asteroids might even be smaller than calculated here. In any case, Pravec and Harris (2000) estimated the error of the size calculation using this method as a factor of 1.5 to 2.

 

Analysis of mutual events between components of a binary asteroid

The existence of a satellite around an asteroid can be derived from an asteroid's lightcurve when a mutual event is observed. This is seen as attenuation in the amount of light reflected from the asteroid during an occultation – when one component blocks the light reflected from the other component, or during an eclipse – when one component casts a shadow over its partner. Therefore, periodicities of the mutual events can be interpreted as due to the orbital period of the secondary around the primary.

Since the light attenuations due to the mutual events are superposed on the lightcurve variability, which is in turn caused by the rotational period of the primary and by its non-spherical shape, the rotational periodicity must first be subtracted from the data so that the orbital periodicity of the secondary can be derived. Therefore, the analysis also includes the following procedures:

  1. Finding the rotation periodicity of the primary, as described above, using data where mutual events are not visible.
  2. Producing a model with the derived rotational properties.
  3. Subtracting the magnitude predicted by the model from all the observed data, including data with mutual events.
  4. Searching for the period of the mutual events using Fourier series analysis (Harris and Lupishko 1989) with the same code used to derive the rotation period. Since the mutual events’ curve is characteristically flat with only two attenuations, as many as 20 harmonics were used to describe its model.
  5. Folding the data with the orbital period of the secondary. Such a lightcurve should present two mutual events (Pravec et al. 2006), usually a total event when the attenuation reaches a plateau before increasing back to the average brightness, and a partial event recognizable by its V-shape (see an example in Fig. A4.5.4).

 

            The properties of the mutual events curve can provide many insights about the characteristics of the asteroid system. A total eclipse/occultation seen in the lightcurve takes place when the light from the secondary is completely blocked by the primary or when the secondary is in front the primary blocking a fixed fraction of its surface. The depth of the total eclipse (Amut) is a function of the two components' size ratio (Rs/Rp):

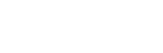                                                                               (15)

when Rs is the radius of the secondary and Rp is the radius of the primary (Polishook and Brosch, 2008).

As the effective radius, R, is a function of the absolute magnitude (see above), it can thus be derived from photometry; the effective radius of each component can also be derived because the effective surface is the sum of the surfaces of the two components, as follows:

                                                                                        (16)
assuming spherical shapes for both components.

The duration of a total eclipse constrains the semi major axis of the secondary's orbit. When the orbital period of the secondary is known, the ratio between the duration of total event to the orbital period should be equal to the ratio between the combined sizes of the asteroid components to the arc of the orbit when the eclipse took place. This can be expressed as:

                                                   (17)

when  is the time of the total event from the time the intensity begins to drop until it raises back to the averaged brightness, is the orbital period of the secondary, Dp and Ds are the effective diameters of the primary and the secondary, respectively, a is the semi major axis of the secondary orbit about the primary and α is the phase angle of the asteroid as seen from the Earth (Pravec et al. 2000). Another option is to use only the time of complete event, only after the attenuation reaches a plateau. In this case, Eq. 17 will change to

                                                   (18).

Equations 17 and 18 are based on several assumptions: the two components are spherical, the viewing aspect is in the orbital plane of the secondary around the primary, thus on the equatorial plane of the primary, the albedos of the primary and secondary are equal, and the effect of the phase angle for the two components is the same. Since these assumptions are only valid on the first order, Eqs. 17 and 18 can only constrain the semi major axis which should be measured by other means such as radar observations or direct imaging with high resolution.

The orbital properties measured and calculated can be used to estimate the physical properties of the primary using the third law of Johannes Kepler, from which the density is derived (and assuming the two components have the density):

                                                                                      (19)
where Mp and Ms are the masses of the primary and the secondary and G is the gravitational constant. This is the only way to get a look inside an asteroid and to learn an important parameter of its composition in absence of an orbiting space probe around the primary. However, one should keep in mind that asteroids are not spherical objects. Thus, even though the mass of an asteroid can be well known, its density, derived by the ratio between the mass and the volume of the body, is only estimated to first order.

 

Inversion photometry to derive the spin axis orientation

Measurements of an asteroid's period using brightness variability are also affected by the aspect angle (ψ) at which the observer sees the asteroid axes. This is defined as the angle between the line of sight (Earth-asteroid) and the asteroid's north pole and is written as:

ψ = 90 – arcsin[sin βse sin βp + cos βse cos βp cos (λse-λp)]                                 (20)
where λse and βse are the ecliptic longitude and latitude of the sub-Earth point (determined by the asteroid's orbit around the Sun), and λp and βp are the ecliptic longitude and latitude of the pole (Tegler et al. 2005). The change in the asteroid brightness can be very small when the asteroid is observed pole-on, or can show a maximal amplitude of the lightcurve when the aspect angle is 900. The aspect angle does change over different geometric conditions of the Earth and the asteroid, so different sides of the asteroid can be seen at different times and at different sidereal years. Therefore, brightness changes over a long period of time and over different aspect angles can reveal the sidereal rotation period of the asteroid, the orientation of the body's axes, its first-order shape and can even suggest the existence of a non-convex object with its bulges and concavities.

            To derive this data we used the convexinv software developed by Mikko Kaasalainen and Josef Durech (http://astro.troja.mff.cuni.cz/projects/asteroids3D/). This software uses as many brightness measurements as possible, obtained over a wide range of viewing geometries, to build a complete model of the asteroid shape, spin parameters and scattering law by solving the inversion problem (Kaasalainen et al. 2001, Kaasalainen and Torppa 2001). The software is given an initial range of axes orientation models and rotation periods and returns a matching χ2 record for each model by:

                                                                                    (21)

when  and  are observed and modeled lightcurves and they are renormalized through the average brightness  and . The software assumes an asteroid with a convex shape, and a simple empirical scattering law, since it was shown by Kaasalainen's papers that concavities have minimal fingerprints on lightcurves and that the role of the scattering law is very minor compared to the pole, period and the shape of the photometric convex hull.

            In addition, Durech et al. (2008a) showed that the software can handle a linear change in the rotation rate, dω/dt, thus it describes an asteroid that rotates by:

ω(t) = ωo + dω/dt · t                                                                                       (22).

This ability allows the discovery of a spun-up (or spun-down) asteroid due to the YORP effect (see chapter 4.1).

            We used this software to derive the spin axes orientations of binary asteroids and separated pairs obtained over large ranges of phase angles and at different apparitions. Measurements at times of mutual events were excluded, since the software cannot handle them. Also excluded were lightcurves of bad quality with low S/N as the software is not sensitive to the photometric errors.

            A χ2 plane for the different axis models tested by the convexinv software were plotted (Fig. 4.8.2 to 4.8.4). Only trial cases with χ2 values at least 10% above the background χ2 values, were considered as possible true solutions. The pole errors were estimated by the χ2 plane of the trial cases, where all models with χ2 of 10% above the background were determined to be within the error range.

 

 

Calculating the colors of the asteroid

For some asteroids, colors were derived to determine the spectral type and to search for color variation while the asteroid rotates ("color curve"). The colors were calculated using the following procedure:

  1. While observing, different filters were switched in different routines (such as V->B->V->R or R->I, etc.).
  2. A color measurement was defined as the magnitude in one filter minus the following magnitude taken in another filter. The magnitudes were used after calibration to a standard magnitude level.
  3. The maximum time between two exposures for color calculation was 12 minutes. This is considered to be too short to influence significantly the color, given typical spin periods of asteroids.
  4. Weighted mean values for each color were calculated for each observing night and were later averaged to determine a representative color for the asteroid.
  5. The colors were compared to the colors listed in the ECAS database (http://www.psi.edu/pds/archive/ecas.html) to derive the spectral type of the asteroid.