פוטומטריה של אסטרואידים:

ניתוח נתונים

האור המגיע מן האסטרואידים יכול ללמדנו רבות על תכונותיהם השונות. הגודל, הצורה, זמן הסיבוב, זווית ציר הסיבוב, הרכב פני השטח, המבנה הפיסי, הצפיפות – על כל אלה ניתן להסיק מתוך מדידת האור המוחזר מפני האסטרואידים. מדע זה מכונה פוטומטריה (מדידת אור) ובבסיסו - עקומת האור – גרף המציג את בהירותו המשתנה של האסטרואיד כפונקציה של הזמן. וכיצד ניתן ללמוד על כל התכונות הללו מעקומות האור? קראו את הטקסט שלהלן, שנלקח מעבודת המחקר שלי ומתאר את כל מה שניתן ללמוד מנקודה קטנה של אור.

1. זמן המחזור העצמי P

הבהירות של האסטרואידים משתנה בצורה מחזורית כפונקציה של הזמן. מחזור זה נגרם עקב סיבוב הגוף סביב עצמו הגורם לשינוי מחזורי בגודל שטח החתך של האסטרואיד המופנה אל הצופה. השינוי בשטח החתך הנראה מעלה ומוריד חליפות את שטף הקרינה שמגיע אל הטלסקופ ומאפשר לאסטרונום לאמוד את תדירות הסיבוב של האסטרואיד. עקומות אור של אסטרואידים, מציגות בדרך ברורה מחזוריות זו (ראו לדוגמה תרשים מס' 1). בנוסף, אזורים על פני הגוף בעלי מאפיינים שונים (דוגמת גודל, אלבדו, מרקם או צבע) יכולים להחזיר את אור השמש בצורה שונה ובכך לייצר מחזוריות במדידת הבהירויות (Pravec et al., 1997). לפי Harris et al. (1989) ו-Pravec et al. (1996), ניתן לעמוד על זמן המחזור של אסטרואיד נתון, ע"י פירוק פורייה להרמוניות של נתוני הבהירות:

H(α,t) = H(α) + [B_n·sin( (2πn/P)·(t-t₀) ) + C_n·cos( (2πn/P)·(t-t₀) )] (1)

כאשר H(α,t) הינו הבהירות של הגוף בזמן t ובזווית מופע α, H(α) הוא הבהירות הממוצעת של הגוף במחזור אחד, B_n ו- C_nהם מקדמי פורייה מסדר n, P הוא זמן המחזור ו-t₀ הוא זמן אפס שרירותי (epoch). ההתאמה הטובה ביותר לביטוי זה מחושבת ע"י מינימיזציה של סכום הריבועים של ההפרשים (Residuals) בין הבהירויות שנמדדו לבהירויות המודל, ומכונה מבחן ²χ:

` (2.a)

משרעת המחזור (Amplitude) A_n מבוטאת מתוך מקדמי פורייה ע"י:

A_n = n = 1…m (2.b)

זווית הפאזה φ_n מחושבת מתוך המקדמים והמשרעת:

cos φ_n = C_n / A_n , sin φ_n = B_n / A_n n = 1…m (2.c)

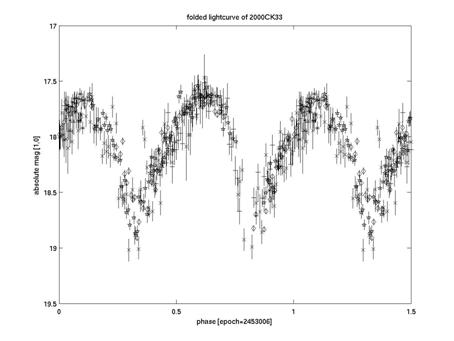
תרשים מס' 1: עקומת אור של האסטרואיד ממשפחת אטן 2000 CK₃₃. ציר ה-X מייצג את מופע הסיבוב (בין 0 ל-1 האסטרואיד השלים סיבוב מלא) וציר ה-Y מייצג את בהירותו המשתנה של האסטרואיד.

2. המחזור הסינודי P_syn, המחזור הסידרי P_sid וה-PAB

מחזור הסיבוב העצמי שחושב בסעיף הקודם הוא המחזור הסינודי, כלומר המחזור שבו הגוף משלים הקפה אחת סביב עצמו מנקודת ראותו של צופה על הארץ, ולא ביחס לנקודה קבועה עבור המחזור הסידרי (למשל מערכת הכוכבים הרחוקים). המחזור הסינודי יכול להשתנות משמעותית עם הזמן עקב המרחק הקצר של אסטרואידים קרובי ארץ לכדור-הארץ ומסלולם האליפטי, הגורמים לשינויים מהותיים במהירותם. ככל שעובר זמן רב יותר בין ליל התצפית הראשון לאחרון, השינוי במחזור הסינודי משמעותי יותר, וכך לא יתאפשר חיבור של עקומות האור מתצפיות אלה בגלל הבדל במופע הסיבוב.

כדי לבדוק אם השינוי במחזור הסינודי איננו גדול מדי ומפריע להתאמת זמן מחזור מדויק, נח להשתמש במושג "חוצה זווית המופע", וכפי שהוא מופיע בספרות ( Harris et al., 1984;Magnusson et al., 1989), ה-PAB (Phase Angle Bi-sector). ה-PAB הוא הוקטור המצביע ממרכז הגוף אל אמצע הקשת המחברת את השמש והארץ (מבחינת האסטרואיד), כלומר הוא חוצה את זווית המופע α. ניתן לדמיין אותו כאנך אל פני הגוף, הנמצא במרכז קרן האור המגיעה מהשמש לזו המוחזרת לכדור-הארץ בהחזרת מראה. Harris et al. (1984), מדגישים את חשיבותו של ה-PAB, לא רק בתור משתנה המאפשר מעבר בין מחזור סינודי לסידרי, אלה כמשמעותי בהבנת שינויים בגיאומטריה של עקומת האור. השינוי dPAB בקואורדינטות האקליפטיות של ה-PAB בין התצפיות לאורך זמן dt, קושרות את המחזור הסינודי למחזור הסידרי לפי הביטוי (Magnusson, 1986):

f_syn = f_sid - dPAB/dt (3)

את השינוי ב-PAB ניתן לחשב על-סמך פרמטרים מסלוליים בלבד ללא ידיעת המחזור הסינודי עצמו (נספח א' על פרמטרים מסלוליים). בתרשים 2, למשל, ניתן לראות את השינוי היומי ב-PAB של האטן CK₃₃ לאורך שנה אחת (2004). השינוי מרבי כאשר זווית המופע α מרבית (180º), כלומר כאשר האסטרואיד נמצא בין השמש לכדור-הארץ, וממילא לא ניתן לצפות בו. ניתן להשוות את השינוי ב-PAB של אסטרואיד קרוב-ארץ לשינוי ב-PAB של אסטרואיד השייך לחגורת האסטרואידים (למשל, 1 Ceres) ולהבחין כי מידת השינוי של אסטרואיד קרוב-ארץ גדולה יותר. לדוגמה, מידת השינוי ב-PAB ביום עבור האסטרואיד קרוב הארץ 2000 CK₃₃ לאורך שלושה חודשים (מ-15 בפברואר ועד ה-15 במאי, 2004) מוצגת בתרשים 3. מידת שינוי זו של כ-10^-3·3.5 ראדיאנים לכל זמן התצפית שקולה לשינוי של 48 שניות בזמן מחזור סינודי של 24 שעות. הבדל זה הוא בטווח השגיאה של זמן המחזור שנמצא מהתאמת פורייה כפי שתואר בסעיף 1 ועל-כן התעלמנו ממנו בחשבון הפוטומטרי שבוצע במחקר זה.

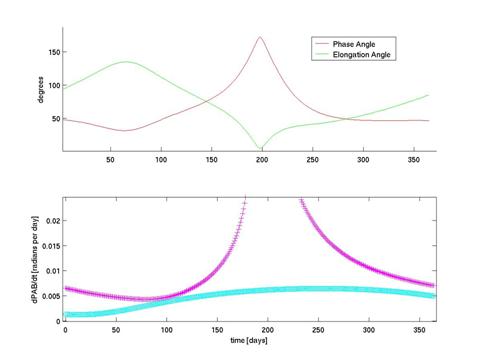
תרשים מס' 2: השינוי ב-PAB ליום של האטן 2000 CK₃₃ לאורך שנה אחת (2004, בצלבים ורודים). השינוי מרבי כאשר זווית המופע α מרבית (בחלון העליון), כשהאטן נמצא בין השמש לארץ. ניתן להשוות את השינוי ב-PAB של האטן לשינוי ב-PAB של אסטרואיד מחגורת האסטרואידים (1 Ceres) ולהבחין כי מידת השינוי של האטן גדולה יותר רוב הזמן (בתכלת בחלון התחתון).

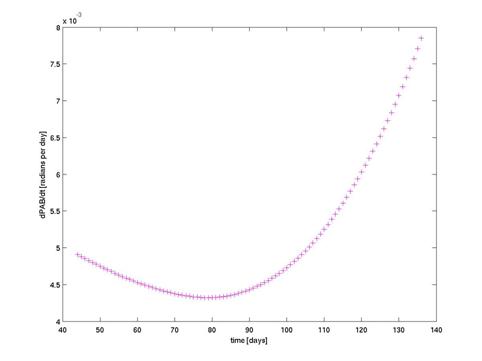
תרשים מס' 3: מידת השינוי ב-PAB ביום עבור 2000 CK₃₃ לאורך שלושה חודשים (מ-15 בפברואר ועד ה-15 במאי, 2004). השינוי של כ-3.5·10^-3 ראדיאנים לכל זמן התצפית שקולה לשינוי של 48 שניות בזמן מחזור סינודי של 24 שעות, פחות מטווח השגיאה, ועל-כן התעלמנו ממנו.

3. תיקון השפעת זווית המופע במערכת H-G

בהירות האסטרואידים תלויה בגורם נוסף – זווית המופע α – הזווית בין השמש לארץ כפי שהיא נראית מהאסטרואיד. כאשר הזווית שווה לאפס, והאסטרואיד, הארץ והשמש נמצאים על אותו הישר (האסטרואיד נמצא ב-"ניגוד" - Opposition), שטח הפנים המואר של האסטרואיד יהיה מרבי מבחינת צופה על הארץ ובהירותו תהיה מרבית. כאשר זווית המופע תגדל, תקטן בהירות האסטרואיד בהתאמה, כפונקציה של שטח הפנים המואר (פונקציה גיאומטרית) אבל גם כפונקציה של מידת החזרת האור (פונקצית פיזור האור). הצגת השינוי בבהירות האסטרואיד כפונקציה של השינוי בזווית המופע מכונה עקומת מופע (Phase Curve), ודוגמה מן הספרות (Harris et al., 1999) מוצגת בתרשים 4 (לרוב מציגים את הבהירות הממוצעת לסיבוב). ניתן לחלק את עקומות המופע לשני חלקים עיקריים: תחום לינארי בזוויות מופע הגדולות מ-7⁰, ותחום אקספוננציאלי מ-7⁰ ומטה. מידת התלילות של התחום הלינארי קשורה באלבדו הגיאומטרי של הגוף – ככל שהעקומה תלולה יותר כך פונקצית הפיזור מתארת כושר לקוי של החזרת האור בזוויות גדולות (אל הארץ), דבר המצביע על אלבדו נמוך. לחילופין, עקומה מתונה מצביעה על אלבדו גבוה.

החלק האקספוננציאלי של עקומת המופע מתאר את "תופעת הניגוד" (Opposition Effect) הנראית כעלייה משמעותית בבהירות סמוך לנקודת הניגוד של הגרם השמימי. תופעה זו, שנצפתה לראשונה ב-1887 בתצפית על טבעות שבתאי, הוסברה בעבר בעזרת הצללה – כאשר השמש, הארץ והגוף נמצאים על אותו ישר, עצמים שונים על הגוף אינם מטילים צל, ובכך הבהירות גדלה. מודלים מורכבים יותר, דוגמת מודל הפיזור הקלאסי של Lumme & Bowell (1981a), לוקחים בחשבון פונקציות פיזור שונות, כמו יעילות החזרת האור של חלקיק בודד (Single Scattering), או של שטח גדול (Multiple Scattering), ומידת ההחזרה לאחור (Back Scattering) על-סמך ההערכות של גודל החלקיקים וצפיפותם, הרכב, נקבוביות והשפעת הטופוגרפיה. המודלים התיאורטים מבוססים הן על ניסויי מעבדה והן על מדידות של כוכבי לכת וירחים שנעשו ע"י חלליות. יתר על כן, התברר שקיימת התאמה מצוינת בין צורת החלק האקספוננציאלי של עקומת המופע לבין הסוג הספקטרלי של הגוף וניתן לספק מעקומה זו הערכה איכותית לאלבדו של הגוף (Belskaya & Shevchenko, 2000).

כדי לתאר באמצעות פונקציה בודדת את עקומת המופע, מתוך מודל הפיזור, אימץ המושב הכללי של ה-IAU ב-1985, את שיטת H-G, המגדירה את בהירות הגוף לפי הביטוי:

H(α) = H – 2.5·log[(1-G)·Φ₁(α) + G·Φ₂(α)] (4)

כאשר H(α) היא הבהירות המופחתת הממוצעת כפי שחושבה בסעיף 1 ו-H היא הבהירות המוחלטת (Absolute Magnitude), שמוגדרת כבהירות המופחתת הממוצעת של האסטרואיד במחזור אחד, במרחק של יחידה אסטרונומית אחת מהשמש ומהארץ ובזווית מופע אפס, ומסומנת ב-H(1,0⁰). G מכונה משתנה השיפוע (Slope Parameter), והוא משמעותי בתיאור תלות הירידה בבהירות כפונקציה של העלייה בזווית המופע. בעוד של-G אין משמעות פיסיקלית מוגדרת, נמצא כי ניתן להשיג התאמה טובה של G ו-H לעקומת המופע על חלקיה האקספוננציאלי והלינארי. בהתאם להחלטת ה-IAU, מוגדר לכל אסטרואיד ערכי H ו-G משלו. ערך של G = 0.15 נבחר כברירת מחדל לגופים שלא נמדד עבורם G. ראוי לציין שלרוב ערכי ה-G ניתנים בין 0 ל-1, אך גם ערכים שליליים או גדולים מאחד אפשריים (Bowel et al., 1989). Φ₁ ו-Φ₂ הן פונקציות של זווית המופע α, המתארות את פיזור האור מחלקיק בודד (Φ₁), ומחלקיקים רבים (Φ₂) לפי:

A₁ = 3.332 A₂ = 1.862 (5)

B₁ = 0.631 B₂ = 1.218

C₁ = 0.986 C₂ = 0.238

W = exp(-90.56·[tan²(0.5·α)]) i = 1,2

φ _iL = exp(-A_i·[tan^Bi(0.5·α)])

φ _iS = 1 -

Φ _i = W·φ_iS + (1 - W)·φ_iL

בזוויות מופע הגדולות מ-30⁰, יש להזניח את W ולהשתמש רק בביטוי φ _iL, כפי שנעשה בעבודות רבות.

תרשים 5 מציג את התרומה של משתנה השיפוע G וזווית המופע α לירידה בבהירות עבור ערכים שונים של G. התרשים מדגים שלזווית המופע תרומה משמעותית לבהירות האסטרואיד וש-G נמוך מפחית במהירות את הבהירות, לעומת G גבוה הגורם לירידה מתונה בבהירות עם העלייה בזווית המופע. העובדה ש-G ו-H יכולים להצביע על האלבדו, הסיווג וגודל האסטרואיד, מספקת להם חשיבות רבה בחקר הפלנטות הקטנות. הבעיה במציאת ערכי H-G עבור גופים מחגורת האסטרואידים היא שיש צורך באיסוף נתונים לאורך חודשים רבים כדי לצפות בגופים בזוויות מופע שונות. לעומת זאת, מכיוון שאסטרואידים קרובי-ארץ נמצאים במסלולים קרובים לארץ (באופן לא מפתיע...), זווית המופע שלהם משתנית במהירות, וניתן להבחין בשינויים בבהירותם תוך מספר שבועות, ולחשב עבורם ערכי G ו-H תוך תקופה קצרה של תצפיות.

מאז שהתקבלה ההסכמה על שימוש בשיטת H-G החלה להישמע גם ביקורת על התאמה זו, ההולכת ומתגברת בשנים האחרונות. הטענות העיקריות העולות כנגד שיטת H-G הינן:

1. התאמת H-G מתעלמת ביסודה מהצורה האליפסואידית של הגוף ומכיוון ציר הסיבוב של האסטרואיד. ייתכן מצב שבו ייראה היטל שונה של הגוף ע"י הצופה באותה זווית מופע אבל בשנה סינודית אחרת (המכונה "הופעה" - Apparition). לפיכך ימדדו G ו-H שונים בהופעות שונות, בהתאם לזווית שבין קו הראייה של הצופה לציר הסיבוב של האסטרואיד (Piironen, 1997).

2. ההתאמה של משוואת H-G איננה תמיד מדויקת ולעיתים היא מספקת נתונים לא עקביים ודו-משמעיים לאסטרואידים הנחקרים, ובפרט לגופים קרובי ארץ, הנובעים מבעיות במודל פיזור האור (Sanna Kaasalainen, 2002). מעבר לכך, ניתן להתאים את עקומת המופע לפיזור הנקודות גם בעזרת פונקציות פשוטות יותר, שאינן מבוססות על מודלים פיסיקלים. Mikko Kaasalainen ועמיתיו (2001) הציעו לבטא את התלות בזווית המופע ע"י משוואה לינארית-אקפוננציאלית לפי:

f(α) = a·exp(-α/d) + βα + b (6.a)

כאשר a הוא הגובה ו-d הוא הרוחב של תופעת הניגוד ו-β הוא שיפוע החלק הלינארי. b הינו קבוע כיול. Belskaya & Shevchenko (2000) ניסחו את החלק האקספוננציאלי באופן שונה:

V(1,α) = V(1,0) – + b·α (6.b)

כאשר a מתאר את גובה תופעת הניגוד ו-b הוא שיפוע החלק הלינארי. V(1,0) הוא הבהירות המוחלטת, במרחק של 1 י"א מהשמש והארץ ובזווית מופע 0⁰, והוא זהה ל-H ממערכת H-G. בלסקיה ושבצ'נקו מצאו גם התאמות בין a ו-b, לאלבדו ולסיווג האסטרואידים.

3. מכיוון שמערכת H-G נבנתה מלכתחילה על סמך תצפיות של גופים מחגורת האסטרואידים, היא מיטיבה לתאר את השינוי בבהירות בתחום של זוויות מופע הקטנות מ-30⁰ לערך. מעבר לתחום זה, אין מידע רב עבור חגורת האסטרואידים (שכן אז הם רחוקים וחיוורים יותר), אבל זהו התחום שבו מרבים לצפות בגופים קרובי ארץ. בתחום זוויות זה גדלה השפעת צורת האסטרואיד ותווים שונים על פניו, וקשה יותר להפריד ביניהם לבין השפעת האלבדו. יחד עם זאת, מחקרים הוכיחו כי ניתן לערוך התאמות פוטומטריות על גופים קרובי ארץ בזוויות מופע גדולות, כפי שנעשה זה זמן רב לגופים בחגורת האסטרואידים בזוויות הקטנות מ-30⁰ (Kaasalainen et al., 2004).

כדי לדלות את מרב הפרטים מהנתונים הפוטומטרים של האסטרואידים במחקר זה, חושבו ערכי ה-G וה-H על-סמך השיטה התקנית, ונעשה גם שימוש במשוואות 6.a-b. כדי להגביר את דיוק החישוב ולהוסיף אילוצים למדידות, נעשתה ההתאמה בו זמנית לזמן המחזור העצמי ולערכי עקומת המופע, ועל-כך בסעיף הבא.

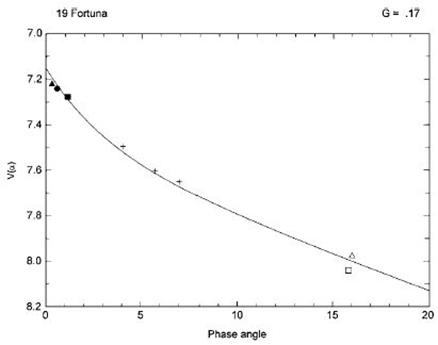
תרשים מס' 4: עקומת המופע של (19) Fortuna מהספרות. ניתן להבחין בנקל בחלק הלינארי של העקומה (גדול מ-7⁰) ובעלייה האקספוננציאלית המכונה תופעת הניגוד (Harris et al., 1999).

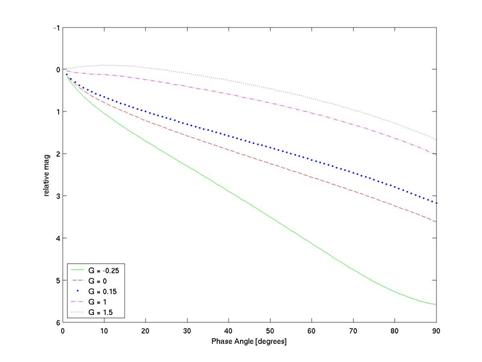
תרשים מס' 5: התרומה של משתנה השיפוע G וזווית המופע α לירידה בבהירות עבור ערכים שונים של G. ניתן להבחין כי לזווית המופע תרומה משמעותית לבהירות הגוף, כאשר G נמוך מפחית את הבהירות במהירות ו-G גבוה גורם לירידה מתונה בבהירות עם העלייה בזווית המופע.

4. התאמה לזמן המחזור העצמי ולמשתני עקומת המופע

התאמת המדידות למודל מייצג נעשתה בשני חלקים נפרדים: עבור זמן המחזור והמשתנים בשיטת H-G, ועבור זמן המחזור ומשוואות 6.a-b. בשני המקרים, כדי לספק אילוצים רבים יותר להתאמה, חוברו שתי המשוואות - משוואת התלות בזמן הסיבוב ומשוואת התלות בזווית המופע. להלן תוצג ההתאמה עבור שיטת H-G, ולאחריה ההתאמה עבור השיטה השנייה.

בשיטת H-G הבהירות המופחתת של האסטרואידים כפונקציה של המחזור העצמי וזווית המופע הינה:

H(α,t) + 2.5·log[(1-G)·Φ₁(α)+G·Φ₂(α)] = H + {B_n·sin[()·(t-t₀)]+C_n·cos[()·(t-t₀)]} (7)

ההתאמה נערכה על סדרה של תדירויות f = 2πn/P וסדרה של משתני שיפוע G, כך שהביטוי נעשה לינארי והקל על חישוב פרמטרי פורייה B_n ו-C_n וערך קבוע עבור H (Kaasalainen et al. 1992). ההתאמה בעלת ערך ²χ מינימלי נבחרה ואיפשרה לנחש סדרות של f ו-G מדויקים יותר להתאמה נוספת וכו'. כל התאמה נעשתה עם פרמטרים שונים לפי הפירוט הבא:

1.) ההתאמה הראשונה נעשתה ע"י power spectrum, כלומר חלוקת ציון לתדירויות שונות ללא התחשבות בהרמוניות אפשריות. בנוסף, לא נעשה שימוש בשגיאות המדידה ובתלות הבהירות בזווית המופע וב-G. תחום התדירויות שנבדק נע בין 0.2 סיבובים ליום עד 12 סיבובים ליום במרווח תדירות של 10^-4·5 סיבובים ליום, בהתאם לתדירויות סיבוב אופייניות של אסטרואידים. צורתה הכללית של עקומת האור סיפקה חסמים מצומצמים יותר לתחום התדירות שנבדק. תדירויות בעלות ציון הגבוה מ-70% מהציון הגבוה ביותר נבחרו להיבדק בשלב הבא.

2.) ההתאמה נעשתה לפי פירוק פורייה להרמוניות (נבדקו עד 6 הרמוניות, בהתאם לצורת עקומת האור) תוך התחשבות בשגיאות המדידה. נבדקו התדירויות שנבחרו בשלב הקודם כולל תחום של 0.2± סיבובים ליום ובמרווח של 10^-4·5 סיבובים ליום. ההתאמה כללה גם אילוץ על זווית המופע ו-G, כאשר G קיבל ערכים בין 1- ל-2 במרווח של 0.01. ערך ה-²χ הקטן ביותר הצביע על תחום של ערכי f ו-G הסביר ביותר.

3.) התאמה דומה עם תחומי בדיקה זהים של f ו-G נעשתה על ערכי הבהירות שהופחתו מהם ההפרשים בין ערכי המודל לערכים שנמדדו (Residuals). הפחתה זו מתקנת שגיאה שיטתית במידה והכיול הסטנדרטי של לילה מסוים לא היה מוצלח בגלל איכות תצפית גרועה בליל הכיול. מערכי הבהירות הופחת הממוצע המשוקלל של ההפרשים של אותו ליל תצפית בלבד (כלומר של אותו השדה).

4.) ערכי f ו-G שהתקבלו מהתאמה 3 נבדקו שוב בתחום של 0.2 מ-G ובמרווחים של 10^-3, ובתחום של 10^-3 מערך ה-f ובמרווח של 10^-5 סיבובים ליום. השגיאות עבור ערכי f ו-G נקבעו על סמך סטיית תקן אחת (68%) ממשטח שווה ²χ. השגיאה של H חושבה לפי ערכי הקצה של G בהתאם למשוואה 19. משטח ²χ לדוגמה מוצג בעזרת קונטורים בתרשים 6. התאמה לדוגמה מוצגת בתרשים 7 על-פני מספר מחזורים. דוגמה להפרשים בין ערכי המודל לערכים שנמדדו (Residuals) מופיעה בתרשים 8 על רקע קיפול המדידות עצמן בהתאם למודל.

התאמת המדידות לפונקציות החדשות (משוואות 6.a-b) של התלות בזווית המופע (סעיף 3) נעשתה בדרך כמעט זהה. מכיוון שבמחקר זה האסטרואידים לא נצפו בתחום זוויות מופע הקטנות מ-7⁰, לתופעת הניגוד אין כל השפעה על המדידות, ולכן ההתאמה נעשתה רק על החלק הלינארי. הפעם, הבהירות המופחתת של האסטרואידים כפונקציה של המחזור העצמי וזווית המופע חושבה כך:

H(α,t) - β·α = H' + {B_n·sin[ ()·(t-t₀) ] + C_n·cos[ ()·(t-t₀) ]} (8)

כאשר α במעלות ו-H' הינה הבהירות הממוצעת לסיבוב בזווית מופע אפס ללא תופעת הניגוד. השלבים השונים של ההתאמה, שתוארו למעלה, בוצעו גם כאן. הערכים שנבדקו עבור השיפוע הלינארי β, נעו בין 0 ל-0.1 במרווח של 10^-5. ערכי השגיאה של התדירות f והשיפוע β נאמדו מתוך קונטורים דומים.

התאמות המודל למדידות שפורטו להלן מספקות ערכים מותאמים היטב לתדירות f ולזמן הסיבוב העצמי הסינודי P, לבהירות המוחלטת H, למשתנה השיפוע G, לבהירות ללא תופעת הניגוד H', לשיפוע הלינארי β ולמשרעת עקומת האור A. אילוץ נוסף לערכים אלו הינו חישובם הנפרד עבור המדידות במסננים השונים B, V, ו-R. קבלת תדירות וזמן מחזור זהים, כמו מופע סיבוב זהה, תאשר את התוצאות. תדירות זהה המתקבלת מתוך ההתאמות לשיפוע עקומת המופע, תחזק את טיב ההתאמה. ערכים דומים של המשרעת אינם הכרחיים לאימות התוצאות. במידה והיו הבדלים בתוצאות, מצוין ההבדל והסיבה לו (לרוב, עקב נתונים מעטים במסנן מסוים). ערכי הבהירות "קופלו" למחזור אחד והם מוצגים כפונקציה של חלק המחזור בצירוף המשתנים שנמצאו בהתאמות.

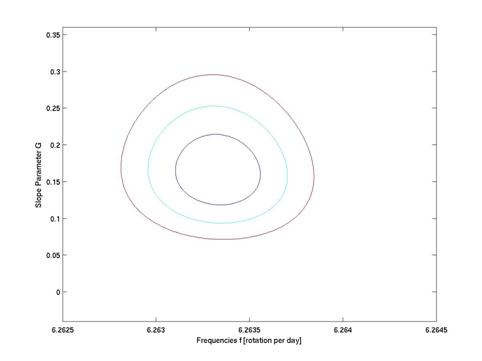
תרשים מס' 6: קונטור השגיאות על משטח ²χ בניסיון להתאים ערכי תדירות הסיבוב העצמי f ומשתני שיפוע G למדידות הפוטומטריות של האסטרואיד 1999 JD₆ במסנן V. הקונטורים מייצגים שגיאות של סטיית תקן אחת (68%) בעיגול הפנימי, שתי סטיות תקן (95%) ושלוש סטיות תקן (99.7%).

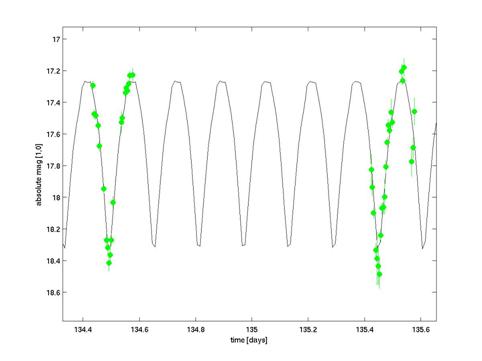
תרשים מס' 7: התאמת מחזור לתצפיות באסטרואיד 1999 JD₆. תצפיות משני לילות עוקבים (ה-14 וה-15 במאי) מוצגות כנקודות על גבי הקו הרציף המייצג את המודל המוצלח ביותר. הגוף נצפה במשך כחודש.

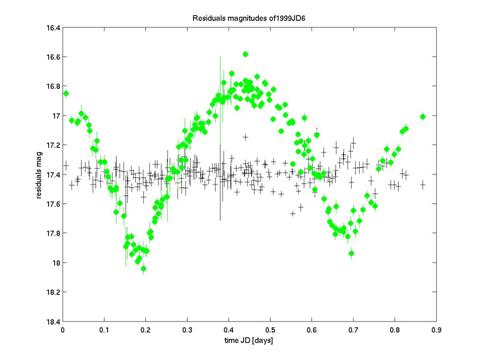
תרשים מס' 8: "קיפול" כל התצפיות של האסטרואיד 1999 JD₆ (דרך המסנן V – בירוק) למחזור אחד. הצלבים השחורים הינם ההפרשים בין ערכי המודל לערכים שנמדדו (Residuals), הקטנים משמעותית ממבנה עקומת האור.

5. חישובי צבעים

כפי שמצוין בסיכום התיאורטי על האסטרואידים, חומרים שונים על פני הגוף יחזירו פסים ספקטרלים שונים באופן שונה, כך ששינוי הקרינה של צבע מסוים יספק מידע על תכונות החומר שעל פני השטח של האסטרואידים ובנוסף יוכל להוסיף אילוצים על חישוב זמן המחזור. על-מנת לעבור לסולם הצבעים נערכו החישובים הבאים:

1.) הצבע חושב כבהירות במסנן אחד פחות הבהירות במדידה הסמוכה במסנן השני. כל מדידה חושבה פעמיים: עם המדידה העוקבת ועם המדידה הקודמת, אם ההפרש ביניהן קטן מ-12 דקות.

2.) הזמן חושב כמחצית הזמן שעבר בין מדידה במסנן אחד למדידה העוקבת במסנן השני.

3.) זווית המופע חושבה כזווית המופע במחצית הזמן בין שתי תצפיות עוקבות במסננים שונים.

ממוצע משוקלל של הצבע נעשה עבור כל לילה בנפרד, על-מנת לקבל צבע אופייני ללילה (אם היו יותר מ-5 ערכים). ערכי הצבעים בכל לילה הושוו זה לזה ונבדקו לגילוי הבדלים ביניהם כדי לחפש שינויים התלויים באלבדו, ולמציאת תבניות היכולות לספק אילוצים נוספים לזמן המחזור. ערכי הצבעים קופלו בהתאם לזמן המחזור המחושב, כדי לזהות שינויים בצבע התלויים בסיבוב (כלומר תלויים באזורים שונים על פני השטח). עקומת צבע (color curve), בתרשים מס' 9, הינה דוגמה לשינוי בצבע כפונקציה של הסיבוב. בנוסף, הוצגו ערכים אלו כפונקציה של זווית המופע כדי לזהות מגמה בשינוי הצבע, התלויה ב-G (Magnusson et al., 1996). כמו כן חושב ממוצע משוקלל לערכי הצבעים לקבלת ערך צבע מייצג עבור האסטרואיד.

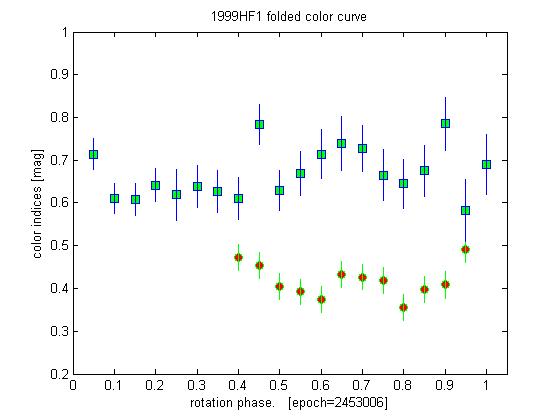
תרשים מס' 9: עקומת צבע של האטן 1999 HF1. הריבועים הירוקים-כחולים הינם בצבע B-V (כחול פחות ירוק), ואילו העיגולים האדומים-ירוקים הינם בצבע V-R (ירוק פחות אדום). שימו לב שבאזור מסוים על פני השטח צבע ה-B-V של האטן עולה (במופע 0.6).

6. צורת הגוף וזווית ציר הסיבוב

ניתוח עקומות האור מספק מידע על שני משתנים פיסיקלים נוספים: צורת הגוף, או היחס בין קטריו השונים, וזווית ציר הסיבוב שלו ביחס למישור המילקה. הפתרונות למשתנים אלו תלויים זה בזה, וניתן ללמוד אותם רק מתוך תצפיות רבות ואוסף של עקומות אור המתארות את האסטרואיד במקומות ובמצבים גיאומטריים שונים מבחינת הצופה. להלן פירוט קצר של שתי שיטות לחישוב המשתנים, המתוארות בהרחבה אצל Magnusson (1986), והיישום שלהן במחקר שלנו.

כאמור, הקרינה המתקבלת מהאסטרואיד תלויה בראש ובראשונה בשטח הפנים שלו המופנה אל הצופה ומחזיר אליו את אור השמש. נוכל להתעלם מהשפעות אחרות דוגמת שינויים באלבדו, פרצסיה או היותו אסטרואיד כפול, במידה וזמן המחזור לאורך התצפיות הינו קבוע (הזנחת הפרצסיה) ולעקומת האור שני שיאים ושני עמקים ללא הרמוניות משמעותיות נוספות והצבע נותר קבוע (האלבדו אינו משתנה). מכאן, שנוכל לתאר את הבהירות לפי שטח הפנים של האסטרואיד המופנה אל הצופה לפי:

M = f – 2.5·log(S) (9)

כאשר S הוא שטח הפנים ו-f הוא פונקציה הכוללת השפעות אחרות (בהירות מוחלטת של הגוף, זווית המופע וכדומה). שטח הפנים של האסטרואיד מותנה במימדיו של הגוף ובזווית ההיטל שלו על מישור הראייה של הצופה. מכיוון שפלנטות קטנות הן בעלות צורה אליפסואידאלית, נוח להגדיר אותן על ידי שלושה צירים וביניהם התנאי a ≥ b ≥ c (Triaxial Body). בנוסף, נוטים לזהות את ציר הסיבוב עם הציר c משום שהוא הציר עם מומנט התמד סיבובי מרבי. זווית ההיטל של האסטרואידים עם הצופה מכונה "זווית ראיית הציר" (Aspect Angle) ומסומנת ב-ψ. זווית זאת מוגדרת בין הציר אסטרואיד-ארץ לבין ציר הסיבוב של האסטרואיד המכוון "צפונה" (z חיובי במערכת קרטזית הליוצנטרית). מכאן, יבוטא שטח הפנים של היטל אליפסואיד (S = π·x·y) ע"י הצירים a, b ו-c וע"י הזווית ψ כך:

S_max = πa (10.a)

S_min = πb (11.b)

כאשר S_max הוא שטח הפנים המרבי במחזור (שיא עקומת האור) ו-S_min הוא שטח הפנים המזערי. בהירות הגוף בשיא עקומת האור תבוטא בעזרת השטח המקסימלי:

H(ψ) = H(90⁰) – 1.25·log[(b/c)²·cos²ψ + sin²ψ] (12)

כאשר H(ψ) הינה הבהירות המוחלטת התלויה בזווית ראיית הציר ψ. התאמה (ע"י ריבועים מינימליים) של המדידות (להלן H(ψ)) למודל של היחס b/c והזווית ψ מכונה שיטת "בהירות-ראיית הציר" (Magnitude-Aspect Method), והיא דורשת מדידות פוטומטריות רבות של הגוף לאורך מספר הקפות, המאפשרות לצפות בו בזוויות ראיית ציר שונות ובזוויות מופע זהות תוך כדי איתור של שינויים בבהירות. התלות של שיטה זו בעקומת המופע (וראו בעיות בקביעתה בסעיף 3) ומשך הזמן הארוך הדרוש להשגת מידע מהימן, הם חסרונותיה העיקריים של השיטה.

דרך נוספת לקביעת צורת הגוף וזווית ציר הסיבוב מכונה "משרעת-ראיית הציר" (Amplitude-Aspect Method), המתאימה שינויים במשרעת הגוף לפרמטרים הדרושים. משרעת עקומת האור A מתוארת ע"י:

A = 2.5·log(S_max / S_min) (13)

בהתאם למשוואות המגדירות את שטחי הפנים S_max ו-S_min תוגדר המשרעת ע"י:

A(ψ) = 1.25·log (14.a)

כאשר A(ψ) היא המשרעת התלויה בזווית ראיית הציר ψ. מאגנוסון מזכיר כי יש להוסיף לביטוי זה את התלות בזווית המופע α, משום שהמשרעת גדלה ככל ש-α גדלה. לטענתו, מתרחשת הצללה רבה יותר במינימה של עקומת האור המפחיתה את הבהירות הכוללת ובכך מגדילה את המשרעת. כדי להתחשב בהשפעה זו במשוואה האחרונה, הוסיף לה מאגנוסון את הביטוי הלינארי מעקומת המופע:

A(ψ) = 1.25·log + β·α (14.b)

מניסיונו, מדגיש מאגנוסון שמשוואה זו מספקת התאמות טובות בעיקר משום ששיטת המשרעת רגישה פחות לתלות בזווית המופע מאשר שיטת הבהירות. בנוסף, מציע מאגנוסון להגדיר את זווית ראיית הציר ψ, כזווית בין ציר הסיבוב של האסטרואיד לוקטור ה-PAB (סעיף 2) במקום לקו הראייה ארץ-אסטרואיד. הגדרה זו מבטיחה טיפול שווה ערך למקור האור ולהחזרתו אל הצופה.

בעיה משותפת לשתי שיטות ההתאמה הינה עקומת אור מורכבת שבה שיא או עמק אחד שונה משמעותית ממשנהו. פיתרון אפשרי הוא לערוך ממוצע על שני השיאים (שיטת הבהירות), או על שתי המשרעות (שיטת המשרעת). בעיה נוספת היא חוסר היכולת לקבוע את מגמת הסיבוב (מזרח או מערב), ואם ערך קו הרוחב של הציר הוא חיובי או שלילי, כך שמתקבלות ארבע אפשרויות לציר אותן ניתן לקבוע על-סמך אילוצים אחרים (למשל ע"י "שיטת הזמנים" – Epoch Method, שלא תתואר כאן).

על-אף שמחקר זה צפה באסטרואידים ממשפחת אטן לאורך תקופה של מספר חודשים, לא נראו משרעות השונות משמעותית זו מזו. בנוסף, המספר המצומצם של משרעות שנצפו (5 משרעות במקרה המרבי) מביא לשגיאות גדולות במיוחד. יחד עם זאת, נעשה ניסיון להתאים את המשרעות הנמדדות מעקומות האור (לאחר שתוקנו ע"י ביטוי זווית המופע β·α) לערכים של יחסי הצירים a/b ו-b/c ולקואורדינטות האקליפטיות של זווית ציר הסיבוב בשיטת "משרעת-ראיית הציר" ע"י ריבועים-מינימליים. חישוב זווית ראיית הציר מתוך קואורדינטות ציר הסיבוב מתואר בנספח א' על הפרמטרים המסלוליים. לצערנו, הנתונים אינם מספקים ועל-כן חושב חסם מזערי ליחס הצירים a/b ע"י:

A = 2.5·log(a/b _min) (15)

ניתן חסם תחתון לקו הרוחב של ציר הסיבוב β_pole, על-סמך התנאים a/b < 5 ו-b/c = 1, שהם תנאים פיסיקלים הגיוניים. קו האורך של ציר הסיבוב נבדק כולו (0⁰ עד 360⁰) והיחס b/c נבדק בתחום שבין 1 ל-2.

7. סיווג ספקטרלי והערכת האלבדו הגיאומטרי

הדרך הטובה ביותר לסווג אסטרואידים הינה על-ידי תצפיות ספקטרוסקופיות ברזולוציה גבוהה, המאפשרות לזהות קווי בליעה של יסודות שונים בספקטרום של הגוף הנצפה. עם זאת, תצפיות כאלו גוזלות זמן רב, דורשות טלסקופים עם מיפתח גדול ולכן לא נעשה בהן שימוש במחקר זה, אלא נעשה ניסיון לסווג את האסטרואידים לפי נתונים שונים הנלמדים מן התצפיות הפוטומטריות: צבעים, ומשתני עקומת המופע. נתונים אלו הושוו והותאמו לנתונים שונים מן הספרות שאפשרו את ביצוע הסיווג.

נתוני הצבעים שלנו (B-V ו-V-R) הושוו לערכי הצבעים מתוך הסיווג של דיוויד ת'ולן. קטלוג הסיווג נלקח מ-PDS. הסיווג של ת'ולן מבוסס על תצפיות שנערכו בין 1979 ל-1983 על 589 פלנטות קטנות במסגרת פרויקט ה-ECAS (Eight-Color Asteroid Survey). במחקר זה נעשה שימוש בשמונה מסננים המכסים אורכי גל מ-0.34 עד 1.04 מיקרון. שלושה מהמסננים (u,b,v) קרובים בערכיהם למסננים סטנדרטים (U,B,V) וחמשת האחרים (s,w,p,x,z) נבחרו משום קרבתם הרבה לפסי בליעה של מינרלים שונים (כמו פירוקסין ואוליבין). הסיבות לבחירת שמונת המסננים מסוכמים היטב בטבלה I אצל Tedesco et al. (1982). הכיול בין ערכי המסננים של ECAS לערכי מסננים סטנדרטים נעשה ע"י עורכי הסקר עצמם בעזרת תצפיות ב-4 כוכבים בעלי ספקטרום זהה לזה של השמש (שם). משוואת הכיול הינה:

B-V = (0.968 ± 0.009) · (b-v) + (0.674 ± 0.003) (16.a)

טבלה 3.3 מציגה את הסיווג של ת'ולן לצד ערכי הצבעים B-V לאחר הכיול. התאמת הצבע v-w לצבע V-R לא נעשתה ע"י ת'ולן ועמיתיו, והנתונים נלקחו מ-Dandy et al. (2003), מלבד השגיאות, שהן ערכי סטיות התקן של הסיווגים ב-v-w (w קרוב בערכו ל-R) כפי שהוצגו בנתוני ECAS.

למערכת התצפיות של ת'ולן נוספו לאחרונה תצפיות חדשות שנעשו על 77 NEOs באמצעות שישה מהמסננים של ECAS. מחקר זה פורסם בעבודת הדוקטורט של רוברט וויטלי (R. Whiteley) כאשר הנתונים ממנו נלקחו גם הם מה-PDS. לא כל סוגי האסטרואידים שנצפו ב-ECAS נראו בקטלוג של וויטלי (A,D,R,T), ולהיפך (V). הסיווג K לא מוגדר בשתי מערכות אלו. טבלה 3.4 מציגה את הסיווג לצד ערכי הצבעים B-V לאחר הכיול (לפי משוואה 30.a) מתוך עבודתו של וויטלי. תרשים 10 מציג את מידת ההתאמה בין שני סיווגים אלו, ומראה דמיון רב בתחום השגיאה (מלבד הסוגים B ו-V). צבעי v-w של וויטלי, כוילו לצבעי V-R, בהתאם ליחס שבין v-w מתוך ECAS ל-V-R של Dandy et al. (2003). היחס הינו לינארי לפי:

V-R = 0.608·(v-w) + 0.371 (16.b)

יש לציין, כי חלק מהאסטרואידים שנחקרו על-ידנו, סווגו בעבר ע"י Bus & Binzel (2002) בעזרת תצפיות ספקטרוסקופיות במסגרת פרויקט SMASSII (Small Main belt Asteroid Spectroscopic Survey, phase II), ומוינו בעזרת מערכת סיווגים חדשה שהשניים פיתחו. מערכת זו, שהתבססה על תצפיות ב-1341 גופים, היא בעלת המדגם הגדול ביותר שנעשה עד היום ובנוסף, היא מתהדרת ברזולוציה גבוהה. בכך, המערכת של באס ובינזל מצליחה לחשוף פרטים חדשים שלא נראו בעבר בספקטרום של אסטרואידים ומאפשרת לזהות קבוצות ותתי קבוצות לא מוכרים בין הפלנטות הקטנות. סקר זה נעשה בתחום אורכי גל של 0.435 עד 0.925 מיקרון ומבחינת המחקר הנוכחי, זהו חסרונו הגדול, שכן הוא לא מאפשר להשוות נתונים שנצפו במסנן B, לתוצאות הסקר.

דרך נוספת לסיווג אסטרואידים באמצעות צבעים היא תצפית בתחום האינפרא-אדום. גם במקרה זה נלקחו ערכים מן הספרות והושוו לסקרים שונים. הסקר 2MASS (2 Microns All Sky Survey) של ה-Infrared Processing and Analysis Center, סרק את כל השמים וסיפק ערכי בהירות במסננים של J, H ו-K (1.24, 1.66, 2.16 מיקרון בהתאמה) עבור יותר מ-470 מיליון גופים ובכללם 12,219 אסטרואידים שזוהו בתמונות הסקר. הנתונים עבור האסטרואידים מופיעים באתר האינטרנט¹ של הפרויקט וכוללים כ-16,000 מדידות (חלק מהגופים נצפו מספר פעמים). במידה והאסטרואידים שנחקרו על-ידנו הופיעו ברשימה זו, חושבו עבורם ערכי צבע J-H ו- H-K, והושוו לערכים תואמים שפירסמו Veeder et al. (1982, 1983) עבור 61 אסטרואידים. בנוסף, הושוו צבעים אלו לצבעי JHK של קבוצות אסטרואידים שונות במאגר של 2MASS (http://www.ipac.caltech.edu/2mass/releases/allsky/doc/ancillary/asteroid.tbl.html).

משתנה נוסף לסיווג אסטרואידים הינו האלבדו הגיאומטרי. ת'ולן ועמיתיו מדדו את האלבדו של כ-250 אסטרואידים מסך הגופים שנצפו ב-ECAS והשתמשו בערך זה בתהליך הסיווג. ערכים ממוצעים של האלבדו לכל סיווג ספקטרלי מובאים בטבלה 3.5 הלקוחה מתוך המאגר של PDS. ערכי אלבדו אלה הושוו עם הערכים התואמים הנלמדים מתוך משתני עקומת המופע: משתנה השיפוע G (ממערכת H-G), שיפוע החלק הלינארי β והיחס בין הבהירות המוחלטת של הגוף עם וללא תופעת הניגוד.

ערכי G הוגדרו כך שיהיו בעלי ערך נמוך עבור גופים בעלי אלבדו נמוך, וערך גבוה עבור גופים בעלי אלבדו גבוה (Bowell et al., 1989). תרשים 11 מציג את ערכי האלבדו כפונקציה של ערך ה-G. ניתן לזהות מגמה המאששת את הקביעה הנ"ל, אם כי יש לציין שהמגמה היא מדויקת לכדי עשירית האלבדו וה-G בלבד ויש אסטרואידים החורגים ממנה. הנתונים שבתרשים מופיעים, ללא שגיאות, במאגר המידע PDS וכוללים 97 אסטרואידים שנמדדו עבורם הן ערכי G והן ערכי אלבדו.

התאמה ישירה בין G לסיווג ספקטרלי נעשתה על 67 אסטרואידים ע"י Skoglöv et al. (1990). בעבודה זו חושבו ערכי G ו-H מתוך נתונים פוטומטרים מן הספרות לפי Bowell et al. (1989). ההתאמה, המוצגת בטבלה 3.6, מאששת את הקביעה כי G נמוך תואם לסיווגים בעלי אלבדו נמוך (דוגמת B, C, F, G ו-P) וגופים עם אלבדו בינוני עד גבוה (E, M, S, R ו-V) הם בעלי G גבוה. מן הראוי לציין, שהשגיאות של G עבור כל סיווג הינן קטנות מהשגיאות שלG עבור כל אסטרואיד. בנוסף, יש לקבל בספקנות ערכי G עבור הסיווגים Q ו-T, שנקבעו על-סמך גוף בודד.

בלסקיה ושבצ'נקו (Belskaya & Shevchenko, 2000) הראו שקיימת התאמה בין הסיווג הספקטרלי למשתנים אחרים של עקומת המופע, דוגמת משרעת תופעת הניגוד והשיפוע של החלק הלינארי β, מכיוון שהאלבדו הגיאומטרי הוא הגורם המשמעותי ביותר בתבנית עקומת המופע (סעיף 3). במחקרם, הם קושרים את האלבדו P_V לשיפוע β לפי:

β = 0.013 (±0.002) – 0.024 (±0.002) · log(P_V) (17)

את טענותיהם ביססו בלסקיה ושבצ'נקו על-סמך מדגם של 33 עקומות מופע של אסטרואידים מחמישה סוגים עיקריים C, E, M, P ו-S, כך שהתאמת אלבדו לערכי β של האתנים הנחקרים איננה שלמה ומפורטת. בנוסף, קובעים השניים כי גובה עקומת המופע הוא פועל יוצא של האלבדו של הגוף: ככל שהאלבדו גדול יותר כך גדלה השפעת הפיזור האחורי (Back-Scattering) לעומת השפעות של הצללה (Shadowing), כך שסופרפוזיציה של שתי השפעות אלה מייצר תופעת ניגוד מרבית עבור אלבדו בינוני. לפיכך, גובה עקומת המופע תלוי באלבדו הקשור בסיווג הספקטרלי. את גובה עקומת המופע ניתן לחשב כמרחק בין שיא תופעת הניגוד (הבהירות המוחלטת, להלן H(1,0⁰)), לבין ההשלכה של החלק הלינארי של עקומת המופע לזווית מופע אפס (להלן H'(1,0⁰)). בלסקיה ושבצ'נקו מציעים כי ניתן לאמוד את הבהירות המוחלטת, במקרים בהם לא ניתן לצפות בגוף במופע אפס, ע"י חיבור פשוט של H'(1,0⁰) לגובה תופעת הניגוד של סיווג האסטרואיד שנחקר. בעבודה זו נעשתה פעולה הפוכה: ערכי H נמצאו מתוך התאמה למערכת H-G ו-H' נמצא ע"י השלכת שיפוע החלק הלינארי β לזווית מופע אפס. ההפרש בין השניים הושווה לנתונים של בלסקיה ושבצ'נקו כדי להתאים את האתנים לסיווג ספקטרלי מסוים. הערכים הממוצעים של האלבדו והשיפוע β מוצגים לצד הסיווג הספקטרלי התואם ומשרעת תופעת הניגוד בטבלה 3.7, שעובדה מתוך מחקרם (טבלאות 1 ו-2, שם).

סייג חשוב בהתאמת האלבדו לשיפוע β ולמשרעת תופעת הניגוד הוא תחום של זוויות המופע הרלבנטי. לפי בלסקיה ושבצ'נקו תחום זה נע בין 5 ל-25 מעלות בלבד והוא קטן מהתחום של חלק מהאסטרואידים הנחקרים. מכיוון שתחום זוויות המופע הגדולות מ-25⁰ לא נחקר דיו כדי לשלול לחלוטין את ההתאמה המוצעת, ההתאמה נערכה לכל האסטרואידים כאשר סייג זה מסומן לגופים הרלבנטים. המדידות של בלסקיה ושבצ'נקו נערכו במסנן V, ולכן השיפוע β ומשרעת תופעת הניגוד שהותאמו הוצאו מתוך עקומות המופע שחושבו לתצפיות במסנן V.

על-סמך ההתאמות שצוינו למעלה התקבלו אפשרויות שונות לסיווג הספקטרלי של האסטרואידים. נעשתה הצלבה בין אפשרויות אלו, שכללה התייחסות למידת ההתאמה, למשקלו של כל מבחן, ולשגיאות בנתונים הפוטומטריים. על-סמך הסיווג הספקטרלי נעשה ניסיון להערכה גסה של המינרלוגיה של פני השטח ומכאן משוערת צפיפות אפשרית ρ של גופים אלה במטרה לעמוד על חוזק המבנה שלהם.

טבלה מס' 3.3: ערכי צבעים של B-V ו-V-R לצד הסיווג הספקטרלי שלהם לפי ת'ולן.

סיווג	מס' גופים במדגם	B-V ^1 ערך מרבי	B-V ^1 ערך מזערי	B-V ^1 ערך ממוצע	V-R ^2 ערך ממוצע
A	4	1.090	0.991	1.039 ± 0.042	0.56 ± 0.07
B	6	0.672	0.639	0.655 ± 0.017	0.36 ± 0.03
C	88	0.746	0.631	0.693 ± 0.025	0.38 ± 0.03
D	26	0.802	0.694	0.735 ± 0.027	0.47 ± 0.02
F	13	0.646	0.594	0.623 ± 0.016	0.37 ± 0.01
G	5	0.765	0.715	0.737 ± 0.021	0.37 ± 0.03
Q	1	0.818	0.818	0.818	0.42
R	1	0.916	0.916	0.916	0.48
S	144	0.955	0.752	0.852 ± 0.041	0.48 ± 0.03
T	4	0.789	0.759	0.772 ± 0.014	0.45 ± 0.02
V	1	0.811	0.811	0.811	0.41
^3 X	73	0.756	0.632	0.701 ± 0.025	0.41 ± 0.02

¹ – הנתונים נלקחו מתוך ה-PDS.

² – הערכים נלקחו מתוך Dandy et al., 2003 והשגיאות, שנלקחו מה-PDS, הן סטיות התקן בצבע v-w.

³ – הסיווג X כולל את הסיווגים E, M ו-P.

טבלה מס' 3.4: ערכי צבעים של B-V ו-V-R לצד הסיווג הספקטרלי שלהם מתוך הסקר של וויטלי ¹.

סיווג	מס' גופים במדגם	B-V ^1 ערך מרבי	B-V ^1 ערך מזערי	B-V ^1 ערך ממוצע	V-R ^2 ערך ממוצע
B	3	0.722	0.688	0.704 ± 0.018	0.39 ± 0.01
C	2	0.738	0.683	0.710 ± 0.039	0.39 ± 0.01
F	3	0.682	0.606	0.639 ± 0.039	0.39 ± 0.02
G	1	0.751	0.751	0.751	0.37
Q	25	0.895	0.752	0.820 ±0.031	0.44 ± 0.04
S	30	0.899	0.790	0.841 ± 0.032	0.47 ± 0.03
V	5	1.006	0.796	0.883 ± 0.087	0.45 ± 0.05
^3 X	8	0.754	0.679	0.712 ± 0.025	0.42 ± 0.02

¹ – הנתונים נלקחו מתוך ה-PDS.

² – הנתונים נלקחו מתוך Dandy et al., 2003, ועברו כיול בהתאם למשוואה 30.b. השגיאות, שנלקחו מה-PDS, הן סטיות התקן בצבע v-w.

³ – הסיווג X כולל את הסיווגים E, M ו-P.

טבלה מס' 3.5: ערכי האלבדו עבור סיווגים שונים, מתוך ECAS ¹.

סיווג	מס' גופים במדגם	אלבדו ממוצע	סיווג	מס' גופים במדגם	אלבדו ממוצע
A	3	0.21 ± 0.099	M	21	0.117 ± 0.036
B	6	0.088 ± 0.021	P	23	0.03 ± 0.006
C	41	0.039 ± 0.009	Q	1	0.21
D	19	0.03 ± 0.005	R	1	0.249
E	8	0.427 ± 0.065	S	73	0.154 ± 0.035
F	10	0.04 ± 0.008	T	1	0.042
G	5	0.055 ± 0.006	V	1	0.249

¹ – הנתונים נלקחו מתוך ה-PDS.

טבלה מס' 3.6: התאמה בין ערכי G לסיווג ספקטרלי של 67 גופים. מתוך Skoglöv et al. (1990).

סיווג	מס' גופים במדגם	משתנה השיפוע G
B, C, F, G, P	24	0.10 ± 0.04
S	25	0.22 ± 0.03
M	12	0.27 ± 0.03
E, V, R	4	0.35 ± 0.05
Q	1	0.10 ± 0.03
T	1	0.27 ± 0.03

טבלה מס' 3.7: ערכי אלבדו, השיפוע הלינארי β של עקומת המופע ומשרעת תופעת הניגוד לפי סיווג ספקטרלי. מתוך Belskaya & Shevchenko (2000).

סיווג	מס' גופים במדגם	אלבדו ממוצע	שיפוע β ממוצע	משרעת עקומת המופע [mag]
C	6	0.07 ± 0.01	0.043 ± 0.002	0.16 ± 0.05
E	4	0.51 ± 0.03	0.020 ± 0.002	0.23 ± 0.03
M	6	0.15 ± 0.02	0.032 ± 0.003	0.34 ± 0.04
P	4	0.04 ± 0.01	0.042 ± 0.002	0.11 ± 0.04
S	10	0.21 ± 0.04	0.029 ± 0.003	0.35 ± 0.04

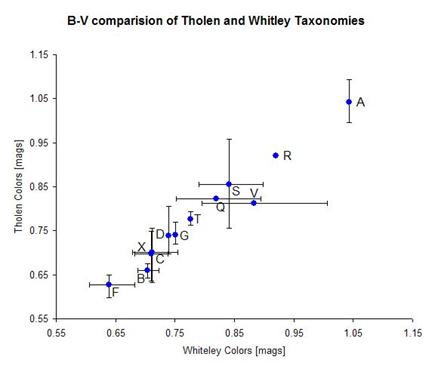
תרשים מס' 10: השוואה בין צבע B-V בסיווגים של ת'ולן ווויטלי. ניתן להבחין בזהות מלאה בין הערכים, בתחום השגיאה (מלבד הקבוצות B ו-V). השגיאה מציינת את הצבע המרבי והמזערי שנמצאו לסיווגים השונים. סיווגים ללא שגיאה נצפו פעם אחת בלבד. המידע נלקח מה-PDS.

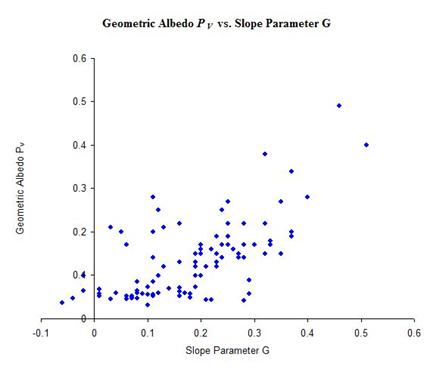
תרשים מס' 11: ערכי האלבדו הגיאומטרי לעומת ערכי משתנה השיפוע G של 97 אסטרואידים. הנתונים הגולמיים נלקחו מאתר האינטרנט של PDS. האתר אינו מספק שגיאות.

8. הערכת גודל הגוף

בהירותם המוחלטת של האסטרואידים (H) במרחק ידוע מהשמש (r) ומהארץ (Δ) ועם אלבדו גיאומטרי משוער (P_V), מספקים את הנתונים הדרושים לחישוב גודלו של הגוף (הרדיוס האפיקטיבי R_eff) בהתאם לבהירות השמש באורכי גל שונים ובהתאם למסננים B, V ו-R:

log(P_B) = 6.521 – 2·log(2R_eff) – 0.4·H_B (18.a)

log(P_V) = 6.259 – 2·log(2R_eff) – 0.4·H_V (18.b)

log(P_R) = 6.247 – 2·log(2R_eff) – 0.4·H_R (18.c)

שתי המשוואות הראשונות מופיעות אצל Bowell et al. (1989) והשלישית עובדה לפי Pravec et al. (1998). מכיוון שנתונה הערכה של האלבדו רק במסנן V (סעיף 7) חושב הרדיוס האפקטיבי מתוך משוואה 32.b בלבד. לסיום, על-מנת לספק מושג על מבנה הגופים, חושבו אורכי צירי האתנים a, b ו-c מתוך הרדיוס האפקטיבי ומתוך יחסי הצירים שחושבו בסעיף 6, ע"י השוואת הנפח האפקטיבי לנפח האליפסואיד:

· R_eff³ = π·a·b·c (19)