פוטומטריה של אסטרואידים:

תצפיות, עיבוד תמונה, מדידות וכיול

האור המגיע מן האסטרואידים יכול ללמדנו רבות על תכונותיהם השונות. הגודל, הצורה, זמן הסיבוב, זווית ציר הסיבוב, הרכב פני השטח, המבנה הפיסי, הצפיפות – על כל אלה ניתן להסיק מתוך מדידת האור המוחזר מפני האסטרואידים. מדע זה מכונה פוטומטריה (מדידת אור) ובבסיסו - עקומת האור – גרף המציג את בהירותו המשתנה של האסטרואיד כפונקציה של הזמן. כיום, הפוטומטריה היא הדרך היעילה והזולה ביותר לחקור את האסטרואידים. להלן מדריך לפוטומטר המתחיל הכוללת תיאור של שיטת התצפית, שלבים בעיבוד תמונה, מדידות וכיול.

תצפית

מטרת הפוטומטריה היא למדוד את בהירותו של האסטרואיד. כיוון שגופים אלו הם לרוב קטנים למדי כדאי להשתמש בזמן חשיפה ארוך כדי לקבל יחס אות / רעש גדול מספיק. מצד שני, כיוון שהאסטרואידים נעים בשמים בקצב מהיר למדי, חשיפה ארוכה תגרום להם לצייר שובל של אור שמקשה על המדידה וגם מוציא את העוקץ מאיסוף של אור באותה נקודה. בנוסף, זמן החשיפה הדרוש תלוי גם בטלסקופ וגודלו, מיקום מצפה הכוכבים, איכות המצלמה, כמות זיהום האור, ותנאי מזג האוויר. במצפה הכוכבים ע"ש וייז, שנמצא באזור עם זיהום אור נמוך, בלילות בהירים ללא ירח, אנו משתמשים בטבלה הבאה בבואנו לקבוע את זמן החשיפה המינימלי הדרוש לתצפית באסטרואידים בעזרת טלסקופ ה-46 ס"מ (C18):

בהירות האסטרואיד	זמן החשיפה
13-14	30 שניות
14-15	60 שניות
15-16	90 שניות
16-17	120 שניות
17-18	150 שניות
18-19	180 שניות

זמני החשיפה הנ"ל הינם הערכה גסה ומשתנים בהתאם למזג האוויר ולתכונות האסטרואיד עצמו. ישנם אסטרואידים שבהירותם משתנה ביותר מיחידת בהירות אחת (magnitude) תוך כדי סיבובם סביב צירם, כך שכדאי לבחור באופן שמרני את זמן החשיפה. זמן החשיפה המרבי נקבע ע"י המהירות הזוויתית של האסטרואיד בשמים וע"י הרזולוציה של המצלמה. אסטרואיד מחגורת האסטרואידים הנע במהירות זוויתית של 0.01 שניות קשת בשנייה, ינוע במשך 180 שניות לאורך 1.8 שניות קשת על המצלמה. היחס של פיקסל / שניית קשת שונה בין מצלמה למצלמה. עם במצלמה שלנו כל פיקסל כולל 0.9 שניות קשת, הרי שבמשך של 180 שניות האסטרואיד ינוע לאורך שני פיקסלים. התנאים האטמוספריים הטובים ביותר במצפה הכוכבים וייז מאפשרים יכולת הפרדה (Seeing) של 2.5 שניות קשת, כלומר כוכב יתפוס כמעט שלושה פיקסלים על המצלמה, ועל-כן אסטרואיד הנע במהירות כזו לא ימרח לכדי שובל. משוואה נוחה לחישוב זמן החשיפה המרבי כדי להימנע ממריחת אור האסטרואיד הינה: Texposure = Seeing / Velocity .

שימוש בפילטרים משנה גם הוא את זמן החשיפה. הנתונים למעלה טובים לפילטר ירוק (V) ואדום (R), אך תצפית באור כחול (B) או בגבול האולטרה-סגול (U) מצריכה זמן חשיפה גדול הרבה יותר התלוי בצבעו של האסטרואיד.

לאסטרונום הצופה באסטרואידים מהירים יש בעיה נוספת – גודל השדה של המצלמה. האסטרואיד שלנו יגמע בשעת תצפית אחת 36 שניות קשת שהן 0.6 דקות קשת. אם גודל השדה של המצלמה הוא 3x3 דקות קשת הרי שלאחר חמש שעות האסטרואיד יעבור את כל שדה הראיה של המצלמה וייצא מתחום הראיה. על-כן, בתצפית של אסטרואידים מהירים יש לרדוף אחר האסטרואיד עם הטלסקופ, או לחילופין להשתמש במצלמה עם שדה רחב. יתרון נוסף לשדה רחב הוא שמלבד האסטרואיד, ניתן לצפות בכוכבים רבים. כוכבים אלו ישמשו אותנו מאוחר יותר לצורך כיול המדידות. במידה ונחליף את השדה עם תנועת האסטרואיד לא נוכל להשתמש באותם הכוכבים לצורך הכיול ובנוסף, ככל שמספר כוכבי הכיול גדול יותר, כך הכיול מדויק יותר.

במקרה של תצפית פוטומטרית של אסטרואידים, שמטרתה לזהות את מחזוריות השינוי בבהירותם, כדאי לדעת את הזמן האופייני של מחזורים אלו. בממוצע, האסטרואידים משלימים סיבוב אחד בכ-6 שעות ולכן כדאי לצפות באסטרואידים במשך זמן ארוך יותר כדי לוודא שתם מחזור שלם. אם זאת, אסטרואידים קטנים סובבים בממוצע מהר יותר, בקצבים של 4 ואפילו 2.5 שעות, ויחד עם זאת, יש מביניהם עם קצב סיבוב איטי מאד של סיבוב ביום (כמו כדור-הארץ שלנו). בכל אופן, תצפית של שעה-שעתיים בלבד לא תאפשר לעקוב אחר מחזור סיבוב שלם ולא תסייע במציאת זמן הסיבוב המדויק של האסטרואיד.

פרמטר נוסף המשפיע על התצפיות הוא גובהו של האסטרואיד בשמים. ככל שהאסטרואיד (או כל עצם אחר) נמוך יותר, כך ההפרעות האטמוספריות רבות יותר ובהירותו של האסטרואיד תרד. אנו צופים באסטרואידים הנעים בגובה של למעלה מ-25 מעלות מעל האופק (מסת אוויר הנמוכה מ-2.5), כדי להימנע מהכחדת אור (light extinction) לא לינארית המסובכת לכיול. כמובן, שאם האסטרואיד נמוך מדי, ניתן לצפות בו ממקום אחר על כדור-הארץ...

עיבוד תמונה

התמונות הדיגיטליות כוללות לא רק את התמונה הנעה של האסטרואידים. יש בהן גם רעשי רקע שונים המשנים את בהירות האסטרואיד וכוכבי ההשוואה. לכן, התמונות עוברות עיבוד תמונה הנחוץ כדי למדוד את ערכי הבהירות האמיתיים של הכוכבים הנצפים:

1. הפחתת Bias – למצלמה יש מתח החשמלי נתון עוד בטרם נחשפה לאור הכוכבים. המתח החשמלי הזה מוסיף קבוע מסוים ושונה לכל פיקסל של המצלמה. כיוון שהרעש הזה הוא סטטיסטי, יש לצלם מספר (5-10) תמונות (להלן תמונות bias) ללא חשיפת צמצם המצלמה לאור, כלומר עם זמן חשיפה אפס. את תמונות ה-bias יש לצלם כאשר הטלסקופ נמצא בחושך מוחלט – הכיפה סגורה, ואור לא חודר מבחוץ. ממוצע חציון של תמונות ה-bias ייתן את מפת ערכי הרעש לכל הפיקסלים של המצלמה. ערכים אלו יופחתו מכל התמונות שצולמו במהלך הלילה.
2. הפחתת dark current – בעת החשיפה החום של המצלמה תורם לרעש הרקע. ככל שהחשיפה ארוכה יותר, יתווסף יותר רעש רקע לתמונה. לכן, יש לצלם מספר (4-5) תמונות dark בזמן חשיפה הזהה לזמן החשיפה של התמונות המדעיות. ממוצע חציון של תמונות ה-dark ייתן את מפת ערכי הרעש התרמי לכל הפיקסלים של המצלמה. ערכים אלו יופחתו מכל התמונות שצולמו במהלך הלילה, בהתאם לזמן החשיפה של כל תמונה. במקרים שבהם המצלמה קרה מאד, ה-dark current הוא נמוך כל-כך שאין צורך בהפחתה זו.
3. החלקת השדה – Flat Field – עיוותים שונים מתווספים לתמונות דוגמת העובדה שמרכז התמונה אוסף כמות אור גדולה יותר משולי התמונה, רגישות שונה לאור של הפיקסלים במצלמה וקיומם של גרגירי אבק על המסננים או על החלון המכסה את המצלמה. צילום של הפרעות אלו בלבד, ע"י צילום של שמים בעת דמדומי השקיעה או הזריחה, יוצרת את תבנית ההפרעות. את ממוצע החציון של מספר (4-5) תמונות flat field יש לנרמל (כלומר, לחלק בממוצע ערכי הבהירות של התמונה) כך שנקבל את היחס של ההפרעות לתמונה חלקה. יש לחלק את כל התמונות המדעיות בתמונת ה-flat field המנורמלת. חלוקה זו תשווה את הבהירות של מרכז התמונה לשוליו, תעלים הפרעות של גרגירי אבק וכדומה.
4. תיקון זמן עריכת התצפית – רוב המצלמות רושמות את זמן תחילת החשיפה במערך הפרמטרים של התמונה. חשוב לשנות ערך זה לזמן אמצע החשיפה על-מנת לייצג בצורה מדויקת יותר את זמן התצפית. בנוסף, כדאי לחשב זמן זה ביחידות של ימים יוליאנים (Julian Days) וחלקיהם, המייצגים את סך הימים שעברו מאז צהרי יום הראשון בינואר 4713 לפני הספירה. יום יוליאני איננו תלוי באורכו של החודש או השנה, ולכן נח יותר לעבוד איתו ולהשוותו למדידות אחרות לאורך זמן. כדאי להשתמש ביום יוליאני במערכת ייחוס של מרכז כדור-הארץ (גיאוצנטרי).
5. יישור התמונות (alignment) – תמונות מאותו השדה אינן תמיד חופפות במדויק זו לזו (עקב בעיות בעקיבה של הטלסקופ, שינוי מכוון בכיוונו ועוד). כדי לאפשר פוטומטריה אוטומטית, יש ליישר (alignment) את התמונות לפי תמונת ייחוס אחת, כך שכוכב מסוים יימצא על אותו הפיקסל בכל אחת מתמונות השדה.
6. פתרון אסטרומטרי (Astrometric solution) - הפתרון האסטרומטרי מאפשר להצמיד קואורדינטות מדויקות לכל פיקסל בתמונה ע"י השוואת התמונה לקטלוג כוכבים מוכר (למשל הקטלוג USNO.A2). ידיעת הפתרון האסטרומטרי של השדה מאפשר לזהות בוודאות כוכבים, אסטרואידים ועוד.

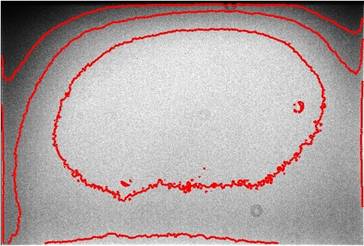
דוגמה לתמונת flat field מנורמלת עם קווי קונטור המסמלים את הבהירות העולה במרכז השדה.

מדידה

מדידת בהירות האסטרואידים נקבעת ע"י מיפתח האזור שנמדד, הפחתת ערך השמים ותרגום מספר האלקטרונים לפוטונים ולערכים בסולם הבהירות האסטרונומי (magnitude) לפי האלגוריתם הבא:

1. קביעת המיפתח (aperture) – סביב מרכז הגוף נקבע מיפתח ברדיוס נתון, וסכום ערכי הקריאות (sum) של כל פיקסל בשטח המיפתח (area) קובע את שטף הקרינה. ככל שהמיפתח גדול יותר כך יגדל הרעש לעומת האות של הגוף הנבדק, וייתכן גם ששטח המיפתח יכיל עצמים אחרים, קרניים קוסמיות או פיקסלים שגויים. לכן, רדיוס המיפתח האידיאלי הינו 4 פיקסלים. יחד עם זאת, מן הראוי למדוד את הבהירות גם ברדיוסי מיפתח נוספים למשל, (6, 8 ו-10 פיקסלים). בנוסף, רדיוס מיפתח גדול (10 פיקסלים) מאפשר להשוות את הנתונים לערכים של כוכבים סטנדרטים שנמדדים עם מיפתח גדול כדי להכיל את כל הפוטונים שהגיעו מהם.

2. חישוב ערך השמים – ערך השמים mSky נקבע מתוך הסביבה הקרובה לעצם הנבדק. טבעת (annulus) ברדיוס פנימי נתון (10 פיקסלים) ועובי נתון (10 פיקסלים) מגדירה את הסביבה הנבדקת. מתוך פיקסלים אלו נזרקים ערכים גבוהים מדי (פיקסלים ברבייה) או נמוכים מדי (פיקסלים שגויים). ממוצע משוקלל על הפיקסלים הנותרים קובע את ערך השמים.

3. שטף הקרינה Flux מחושב לפי הפחתת ערך השמים מערכי הקריאות שבמיפתח: Flux = sum – area · mSky

כאשר sum הוא סכום הקריאות כולל ערך השמים, area הוא שטח המיפתח בפיקסלים רבועים, ו-mSky הוא ערך השמים לפיקסל שחושב למעלה.

4. הבהירות Mag חושבה לפי: M = – 2.5·log(Counts / time) + ZP

כאשר Counts הוא מספר קריאות הפוטונים שנמדדו בשטח המיפתח, time הוא זמן החשיפה בשניות, ו-ZP הוא נקודת אפס שרירותית (עבור הטלסקופ במצפה וייז הערך הינו 22 mag בקירוב).

5. שגיאת הבהירות ΔM מחושבת כפונקציה של רעש המצלמה, השגיאה בחישוב השמים ושטף הקרינה לפי:

ΔM = 1.0857 · / Counts

כאשר Counts הוא מספר הקריאות שנמדדו בשטח המיפתח, epadu הוא ערך ה-Gain (יחס בין האלקטרונים לפוטונים) של המצלמה, area הוא שטח המיפתח בפיקסלים רבועים, stdev הוא סטיית התקן של ערך השמים ו-nsky הוא מספר הפיקסלים עם ערכי שמים.

6. יש לנפות מהתוצאות מדידות שגויות שנגרמו עקב קירבה צמודה מדי בין האסטרואיד לכוכב מזדמן, קרניים קוסמיות שנפלו בשטח המיפתח וכיוצא בזה.

שתי עקומות אור של האסטרואיד 1999 JD₆ שנמדדו בעזרת מפתחים עם רדיוסים שונים (ירוק - 4 פיקסלים, ושחור - 10). ברוב התמונות נשמר יחס בהירות דומה בין המיפתחים, אך לעיתים נכנס למיפתח מקור אור אחר דוגמת כוכב (בתמונה) הגורם לעלייה מדומה בבהירות האסטרואיד (מסומנת בחיצים).

כיול

השפעת אטמוספרת הארץ על התצפיות

בהירות הגוף המתקבלת עבור כל תמונה איננה ניתנת להשוואה עם הערכים שנמדדו בתמונות האחרות עקב שני גורמים אטמוספריים המשתנים במהלך התצפית ומשנים את ערך הבהירות בין התמונות: מסת האוויר ומזג האוויר.

מסת האוויר (Air Mass) היא הכמות היחסית של האטמוספרה בין הטלסקופ לעצם הנצפה. עוצמת האור של העצם מופחתת בגלל פיזור האור ע"י מולקולות האוויר וחלקיקי האבק שבאטמוספרה, והטלסקופ אוסף פחות פוטונים. ככל שקרני האור עוברות דרך עמודת אטמוספרה גדולה יותר, מספר הפוטונים הנמדדים מהמקור הולך ויורד וההפחתה בעוצמת האור (Extinction) גדולה יותר. כאשר העצם הנצפה נמצא בזנית, עמודת האטמוספרה בין הטלסקופ לגרם השמימי הינה מזערית, וכאשר העצם נראה באופק עמודת האטמוספרה הינה מרבית. מסת האוויר X מחושבת מתוך הזווית Z שבין הזנית לזווית הגובה של הטלסקופ: X = 1/cos(Z). מכאן, שמסת האוויר המזערית שווה ל-1 כאשר הטלסקופ מכוון לזנית, והיא אינסופית כאשר הטלסקופ מופנה אל האופק. מכיוון שכיפת השמים והעצמים הנראים בה נעים ממזרח למערב, זווית הגובה בה הם נצפים משתנה במהלך הלילה, כך שבהירות הגוף מבחינת הצופה תלך ותרד ככל שהוא יתקרב אל האופק ללא קשר לבהירותו האמיתית. בגלל שעבור מסת אוויר גבוהה, ההפחתה גדלה אקספוננציאלית, ונדרשים תיקונים משמעותיים מסדר שני, נבחר בעבודה זו חסם של 2.5 כמסת אוויר מרבית, שהיא כ-24 מעלות מעל לאופק.

לעניינינו, מזג האוויר הוא סך התנאים האטמוספריים בזמן התצפית, הכוללים הימצאות של חלקיקי אבק, אדי מים, אובך, עירבול תרמי ועוד, בין הטלסקופ לעצם הנצפה. ככל שהאטמוספרה "מלוכלכת" יותר, כך בהירות הגופים תקטן וכמות אור הרקע תגדל. הקשר בין מסת האוויר לתנאים האטמוספריים מוגדר ע"י הביטוי kX, כאשר X היא מסת האוויר ו-k הוא קבוע ההכחדה (extinction factor), שהינה פונקציה של התנאים האטמוספריים בזמן התצפית. בעזרת הביטוי kX, ניתן לחשב את השינוי בבהירותו של העצם הנצפה, בעזרת המשוואה:

M_apparent = m_instrument + kX

כאשר m_instrument הינו "הבהירות המכשירית" – הבהירות הנמדדת של העצם הנצפה, ו- M_apparent הינה "הבהירות הנראית", כלומר בהירות העצם כפי שהייתה נמדדת ללא ההפרעות האטמוספריות. מכיוון שהתווך האטמוספרי מגיב בצורה שונה לגלים בתדרים שונים, ולחילופין לצבעים שונים, יש לחשב את הבהירות הנראית של העצם הנצפה בנפרד לכל צבע:

B_apparent = b_instrument + k_bX

כאשר, למשל, b_instrument ו-B_apparent הינן הבהירות המכשירית והנראית של העצם תחת מסנן כחול (B), ו-k_b מתאר את מידת ההפחתה האטמוספרית של הצבע הכחול.

מכיוון שתנאי מזג האוויר משתנים עם המקום והזמן, יש לכייל את התמונות לפי אותם תנאים אטמוספריים, ולהצמיד את כל התצפיות לסולם אחיד כך שניתן יהיה להשוות ביניהן. כדי לעבור לסולם כזה יש לקבוע את ההפרש בינו לבין סולם הבהירויות המסוים. הפרש זה מכונה "סטייה מנקודת האפס" (Zero Point offset - ZP) ויש להוסיף אותו למשוואת הבהירות:

M_apparent = m_instrument + kX + ZP

כיול יחסי (Relative Calibration)

את השפעת ההכחדה האטמוספרית ניתן לתקן גם באופן יחסי באמצעות השוואה לתמונת ייחוס משדה נתון, ללא מדידה או חישוב של ערך מסת האוויר, קבוע ההפחתה או נקודת האפס, כפי שמתאר האלגוריתם הפשוט הבא. מתוך מאגר התמונות נבחרה תמונה אחת, להלן "תמונת הייחוס" (באיכות טובה, עם מסת אוויר נמוכה יחסית בין 1 ל-2), ומתוכה נמדדו פוטומטרית מספר מרבי של כוכבים, להלן "כוכבי השוואה" (על בחירתם בהמשך). בנוסף, נמדדו אותם כוכבי השוואה בשאר התמונות מאותו השדה. מדידה פוטומטרית זו נעשתה באותה השיטה ועם אותם הפרמטרים (רדיוס מיפתח, טבעת השמיים, וכו') שבהם נמדד הגוף הנחקר. עבור כל כוכב השוואה i, חושב ההפרש
Mdiff _i,j בין בהירותו Mstar _i,j בתמונה j, לבין בהירותו בתמונת הייחוס, Mref _i:

Mdiff _i,j = Mstar _i,j - Mref _i

השגיאה בהפרש הבהירויות חושבה כשורש הסכומים הריבועיים של שתי המדידות:

ΔMdiff _i,j =

על הפרשי הבהירויות ושגיאותיהן בתמונה j נעשה ממוצע משוקלל:

<Mdiff> _j =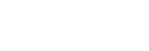

Δ<Mdiff> _j =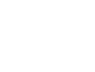

כאשר <Mdiff> _j הוא הפרש הבהירויות הממוצע של תמונה j מתמונת הייחוס, ו- Δ<Mdiff> _j הינו שגיאת ההפרש הממוצע. חשוב לציין שהממוצע לא נעשה על ערכי הבהירויות הנמצאות בסולם לוגריתמי, כי אם על ההפרש ביניהן. ההפרשים זהים בעיקרון זה לזה עד כדי תחום השגיאה. כדי לוודא שהממוצע לא נעשה בעזרת כוכב עם בהירות משתנה, נבדק המרחק בין הפרש הכוכב i לבין החציון של כל ההפרשים בתמונה j. במידה ומרחק זה גדול מ-0.02 mag, הכוכב הוצא ממערך כוכבי ההשוואה בתמונה הנבדקת.

את הפרש הבהירויות הממוצע לתמונה j נחסיר מבהירותו של העצם הנחקר Minst _j:

Mrel _j = Minst _j - <Mdiff> _j

כאשר Mrel _j היא הבהירות היחסית של העצם הנחקר. שגיאת הבהירות היחסית תחושב מתוך שורש הריבועים של שגיאת הפרש הבהירות הממוצעת לתמונה ושגיאת בהירות העצם, ΔMinst _j:

ΔMrel _j =

כעת, כל התמונות מאותו השדה מכוילות לפי תמונת ייחוס אחת וניתן להשוות את ערכי העצם הנחקר בהן, למשל אסטרואידים, ולצייר את עקומת האור של הבהירויות היחסיות כפונקציה של הזמן. על-מנת לבדוק את איכות הכיול היחסי, רצוי לכייל בהירויות של כוכבים נוספים בשדה באותה הדרך בה כוילה בהירות הגוף הנחקר. הבהירות המכוילת של כוכבים אלו איננה אמורה להשתנות כפונקציה של הזמן (בניגוד לבהירות האסטרואידים, כאמור) כך שעקומות האור שלהם יראו כקו ישר עם שיפוע אפס בתחום השגיאה. תמונה שבה כל ערכי הבהירויות חורגות מהישר לא כוילה באופן ראוי. את כוכבי ההשוואה כדאי לבחור לפי העקרונות הבאים: (i) כוכבים שאינם ברוויה, (ii) כוכבים שנמצאים בכל תמונות השדה, (iii) כוכבים במגוון בהירויות ביחס לאסטרואיד הנחקר.

חשוב לזכור כי ערכי הבהירות שחושבו נמצאים בסולם בהירות לוגריתמי רגיל, שנקודת האפס שלו (Zero Point) היא שרירותית, ולכן לא ניתן להשוות את התוצאות עם בהירויות משדות תצפית אחרים. מכיוון שמהירותם הזוויתית של האסטרואידים בכיפת השמים גבוהה מאד ביחס לכוכבי ההשוואה, הם יכולים לחצות בלילה בודד שדות הגדולים משדה הראיה של המצלמה, כך שבכל לילה האסטרואיד נצפה בשדה אחר.

כיול סטנדרטי לפי כוכבי לנדולט (Landolt Equatorial Standards)

על-מנת לכייל את כל התצפיות לסולם בהירות אחיד יש צורך למדוד את הסטייה שלהן מנקודת האפס. הכיול מתבצע ע"י צפייה בשדות שנראים בהם כוכבים סטנדרטים (Standards) שבהירותם המכוילת ידועה וקבועה (כלומר, לא מדובר בכוכבים המשנים את בהירותם חליפות). מתוך ידיעת בהירותם המכוילת וההשוואה לבהירותם הנמדדת, ניתן לחלץ את הסטייה מנקודת האפס, ZP:

M_calibration = m_instrument + kX + ZP

כאשר M_calibration הינו הבהירות הנראית הידועה של הכוכב הסטנדרטי, m_instrument הינו בהירותו הנמדדת, ו-kX מתאר את השינוי בבהירות כפונקציה של מסת האוויר. את תצפיות הכיול יש לעשות במקביל לתצפיות בשדות הנחקרים, ובלילה פוטומטרי – כלומר לילה נקי מעננות ואובך. יש לציין, שגם נקודת האפס תלויה בצבע, ועל כן חשוב לבצע כיול סטנדרטי ע"י צפייה בכוכבים בצבעים שונים. כיום קיימים קטלוגים של כוכבים סטנדרטים המאפשרים לאסטרונום לערוך את הליך הכיול בקלות יחסית. המפורסם והיעיל מבין הקטלוגים הללו הוא קטלוג הסטנדרטים המשווניים של לנדולט (Landolt, 1992), שברשימתו אסף סדרות של כוכבים סטנדרטים הקרובים זה לזה בשמים, כך שתצפית בכולם יחדיו חוסכת זמן תצפית יקר. סדרות פוטומטריות אלו מפוזרות באופן אחיד לאורך המשווה השמימי, כך שניתן לצפות בהם בזמנים שונים בשנה הן מהמחצית הצפונית והן מהמחצית הדרומית של כדור הארץ.

מכיוון שהאסטרואידים נצפים בשדות שונים בכל לילה, יש צורך לבצע כיול סטנדרטי עבור כל שדה בנפרד. יש לצלם את שדות כוכבים אלו עם הפילטרים הרלבנטיים, במסות אוויר שונות (1~, 1.5~, 2~, 2.5~) פעמיים-שלוש כל שדה, בזמן חשיפה של 60 שניות. במקביל לתצפית בסדרות של לאנדולט יש לצלם את השדות בהם נצפו האסטרואידים בלילות קודמים על-מנת לקבל ערכים פוטומטריים מכוילים של כוכבי ההשוואה שנבחרו, כמתואר בסעיף הקודם.

כדי לעמוד על סך הבהירות של הכוכבים הסטנדרטים יש למדוד אותם במיפתח שקוטרו 10 פיקסלים, וכמוהם למדוד את כוכבי ההשוואה. את בהירות הכוכבים הסטנדרטים שנמדדו יש להתאים לבהירות הידועה שלהם בשיטת "ריבועים מינימליים" ולמצוא את המשתנים הפוטומטרים של ליל התצפית, עבור כל צבע (B, V, R), למשל:

V = -2.5·log(Counts / time) – ZP - k _(b-v) X

כאשר V הוא הבהירות המכוילת של הכוכב הנצפה במסנן ירוק (למשל), Counts הינו סך המניות שנאספו, time הינו זמן החשיפה של התמונה הנתונה ו-X הינו מסת האוויר בה צולם השדה. ההתאמה מספקת את ZP, שהוא הסטייה מנקודת האפס של סולם הבהירויות הסטנדרטי ואת k _(b-v) שהוא קבוע ההכחדה עבור צבע נתון. בנוסף, ההתאמה מפחיתה מצדה הימני של משוואת הבהירות ביטוי מסדר שני עבור ההבדל בצבע של הכוכבים הנמדדים Color (למשל B-V) מתוך המשוואה בסדר ראשון:

V = -2.5·log(Counts / time) – ZP - k _(b-v) X – Color * Color Term

כאשר Color Term הוא מקדם להבדל בצבע.

לאחר שנמצאו המקדמים של משוואת הבהירות, יש להציב בה את משתני התצפית השונים של כוכבי ההשוואה, על-מנת לקבל עבורם ערכים פוטומטריים מוחלטים. עבור שדות שנצפו דרך מספר מסננים (למשל B, V, R) ניתן לחשב את תיקון הצבע מסדר שני פעמיים לכל צבע. עבור מסנן V למשל, נמדד התיקון גם לפי B-V וגם לפי V-R. במידה ותיקון הצבע זהה בשני הצבעים שונה משמעותית, הרי שכוכב ההשוואה לא כויל כהלכה.

את הערכים המכוילים של כוכבי ההשוואה מלילות הכיול יש להתאים לערכי הבהירות היחסיים של אותם הכוכבים מלילות התצפית הרגילים כדי למצוא את הסטייה מנקודת האפס של כל לילה. עבור כל כוכב השוואה i, יש לחשב את ההפרש בין בהירותו בתמונת הייחוס מליל התצפית הרגיל Mref _i לבהירותו המכוילת Mcal _i:

Mdiff _i = Mref _i - Mcal _i

השגיאה בהפרש הבהירויות מחושבת כשורש הסכומים הריבועיים של שתי המדידות:

ΔMdiff _i =

מתוך הפרשי הבהירויות ושגיאותיהן נחשב ממוצע משוקלל <Mdiff>. ניתן לבצע ממוצע זה על ערכים בסולם לוגריתמי מכיוון שההפרשים קרובים מאד זה לזה. יש להוציא מהליך הכיול כוכבים פעילים ומשתנים שההפרש בין בהירותם בליל הכיול לבהירותם בליל התצפית רחוק מחציון ההפרשים של כל כוכבי ההשוואה. יש לוודא, כמובן, שבתהליך ניפוי כוכבי השוואה בעייתיים נותרים מספיק כוכבי השוואה לביצוע הכיול.

את הממוצע <Mdiff> מפחיתים מערכי הבהירות היחסית של האסטרואידים Mrel _j בכל תמונה j:

Mcal _j = Mrel _j - <Mdiff>

כאשר Mcal _j הינו הערך המכויל של האסטרואיד הנבדק בתמונה j. חשוב לציין ש- Mrel _jהוא ערך הבהירות שתוקן ע"י תמונת הייחוס, כפי שתואר למעלה. שגיאת הבהירות המכוילת של האסטרואיד ΔMcal _j בתמונה j מחושבת ע"י שורש סכומי הריבועים:

ΔMcal _j =

כאשר ΔMrel _j הינו שגיאת הבהירות של האסטרואיד הנבדק בתמונה j, לאחר התיקון היחסי, ו- Δ<Mdiff>הינו השגיאה המשוקללת של הפרשי הבהירויות שחושבה למעלה.

תיקון המרחק והזמן

האור שנקלט ע"י הצופה מהאסטרואידים מגיע מן השמש ומוחזר מפניהם אל הארץ. לכן בהירותם הנראית של האסטרואידים תלויה בשני גורמים נוספים: מרחקם מהשמש ומרחקם מכדור-הארץ. כיוון שעוצמת האור קטנה ביחס הפוך לריבוע המרחק, יש להפחית מהבהירות הנראית של האסטרואיד הנחקר את השפעת מרחקו מהשמש r ומרחקו מכדור הארץ Δ בדרך הבאה:

H(1,α) = Mcal – 2.5·log(r²·Δ²)

כאשר Mcal היא הבהירות המכוילת של האסטרואידים כפי שחושבה בסעיף הקודם ו-H(1,α) מכונה "הבהירות המופחתת" (Reduced Magnitude) ומוגדרת כבהירות האסטרואידים במרחק של יחידה אסטרונומית אחת מהשמש ומכדור הארץ. המרחקים r ו- Δמוגדרים ביחידות אסטרונומיות. לרוב (למשל אצל Bowell et al., 1989) מופיעה המשוואה הנ"ל בצורה:

H(1,α) = Mcal – 5·log(r·Δ)

שיטת חישוב המרחק של אסטרואיד מהשמש ומכדור הארץ מוסברת כאן.

מרחקם המשתנה של האסטרואידים מכדור-הארץ משנה גם את הזמן בו לוקח לקרני האור להגיע לצופה (light travel time). כדי לכייל את התצפיות לאותו סולם זמנים, יש לתקן את זמן התצפית הארצי לזמן בו קרני האור עזבו את הגוף הנצפה. התיקון הפשוט תלוי במרחק האסטרואיד מכדור הארץ Δ ובמהירות האור c:

JDast _j = JDobs _j – Δ _j/c

כאשר JDast _j הוא הזמן בו עזבו קרני האור את האסטרואיד ו- JDobs _j הוא הזמן בו נקלטו קרני האור בטלסקופ בתמונה j.

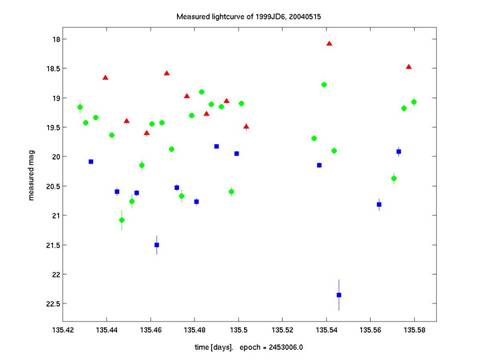
הבהירות הנמדדת של 1999 JD₆ לפני תהליך הכיול כפונקציה של הזמן בליל ה-15 במאי, 2004. ערכי הבהירות הם שרירותיים ביחס לנקודת האפס. ציר הזמן מתחיל בצהרי הראשון בינואר, 2004 UT (JD=2453006). ריבועים כחולים מייצגים מדידות במסנן B, עיגולים ירוקים ב-V ומשולשים אדומים ב-R. הבהירות הנמדדת מושפעת מהשינוי במסת האוויר ומהתנאים האטמוספריים בעת התצפית. שימו לב ל-"בלגן" של הנקודות...

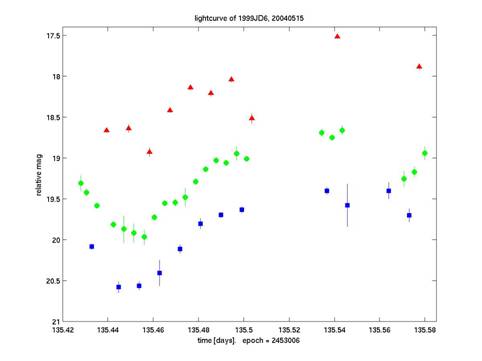
עקומת האור של 1999 JD₆ מליל ה-15 במאי, 2004 לאחר הכיול היחסי. הצורה הסינוסיאידלית של העקומה נראית בברור כבר בשלב זה של הכיול.

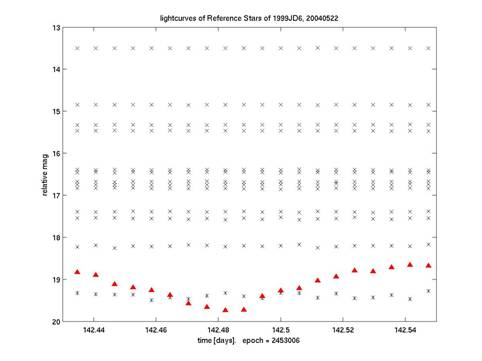
כיול יחסי של בהירות כוכבים בשדה לפי אותו הכיול שנעשה לאסטרואידים. בהירותם של הכוכבים (איקסים) קבועה בתחום השגיאה ומציירת לרוב עקומה ישרה, בעוד עקומת האור של האסטרואיד (משולשים אדומים) היא בעלת תבנית מחזורית.